




Лекция 10
Осциллятор с сильной диссипацией.
Быстрые и медленные движения
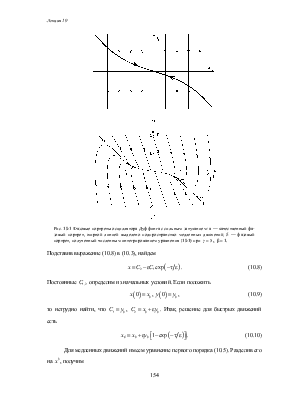
В предыдущей лекции мы сосредоточили свое внимание на системах близких к линейным консервативным. Это позволило представить решение в виде квазигармонических колебаний с медленно меняющимися амплитудой и фазой. Теперь затронем еще один важный класс задач: сильно нелинейные колебания в сильно неконсервативных системах, для которых можно выделить временные интервалы с качественно различным характером изменения переменных — участки быстрых и медленных движений. Типичный пример представляют подобные релаксационные автоколебания (см. рис. 1.1). Более подробно они будут рассмотрены в лекции 11. Здесь же мы продемонстрируем метод приближенного анализа, основанного на разделении быстрых и медленных движений, для осциллятора Дуффинга с сильной диссипацией
x+2γx +x+βx3 =0, (10.1) где γ — большой параметр. Для определенности будем считать β > 0 (осциллятор с «жесткой» пружиной, см. лекцию 8).
Введем
новое время τ = t![]() 2γ
.
Уравнение (10.1) примет вид
2γ
.
Уравнение (10.1) примет вид
εx′′+ x′+ x +βx3 = 0, (10.2)
![]() где ε
=14γ
2
<<1
— малый параметр, штрихи обозначают дифференцирование по τ.
Таким образом, мы получили уравнение, содержащее малый параметр при старшей
производной. Именно такие системы удобно анализировать при помощи метода
разделения быстрых и медленных движений.
где ε
=14γ
2
<<1
— малый параметр, штрихи обозначают дифференцирование по τ.
Таким образом, мы получили уравнение, содержащее малый параметр при старшей
производной. Именно такие системы удобно анализировать при помощи метода
разделения быстрых и медленных движений.
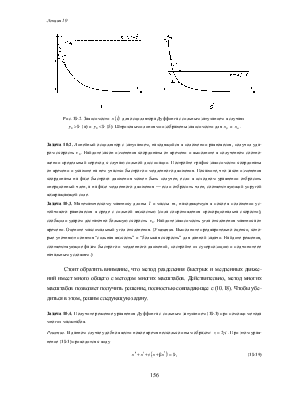
Задача 10.1. Для линейного колебательного контура, состоящего из последовательно соединенных индуктивности L, емкости C и сопротивления R, получите условие сильной диссипации в явной форме.
Перепишем уравнение (10.2) в виде системы двух уравнений первого порядка
|
x′ = y, |
(10.3) |
|
εy′ = −y − x −βx3 = f (x y, ) . |
(10.4) |
Из уравнения
(10.4) видно, что y′ = f
(x
y,
)![]() ε
>>1
везде, за исключением области, где функция
ε
>>1
везде, за исключением области, где функция
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.