


ЛАБОРАТОРНАЯ РАБОТА №2
Изучение электрических свойств сегнетоэлектриков
Выполнил: , 121 группа
2003 г
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
Цель работы: изучение поляризации сегнетоэлектриков в зависимости от напряженности электрического поля Е, получение кривой e (E), изучение диэлектрического гистерезиса, определение диэлектрических потерь.
МЕТОД ИЗМЕРЕНИЯ
Напряжение U, снимаемое с потенциометра R3 и являющееся, по сути, переменным на фоне постоянной составляющей, подаётся на емкостной делитель C1 C2.
Поскольку С1 и С2 соединены последовательно, они имеют одинаковый заряд q на обкладках. Величина этого заряда может быть выражена через электрическое смещение поля D в исследуемом конденсаторе С1: D =d= q/S. Отсюда:
q = DS, (1.13)
где 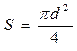 –
площадь обкладок конденсатора С1,
d – его диаметр, d – поверхностная
плотность заряда на обкладках С1.
–
площадь обкладок конденсатора С1,
d – его диаметр, d – поверхностная
плотность заряда на обкладках С1.
На пластины вертикального отклонения луча осциллографа подается напряжение UY , снимаемое с эталонного конденсатора С2:
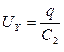 , (1.14)
, (1.14)
а с учетом (1.13):
![]() (1.15)
(1.15)
На пластины горизонтального отклонения луча осциллографа подается напряжение UX , снимаемое с делителя R1 R2, необходимого для приведения напряжения U к рабочему диапазону входных напряжений горизонтальной развёртки осциллографа:
![]() (1.16)
(1.16)
Емкости С1, С2 подобраны таким образом, что С1 << С2 . Поэтому с достаточной степенью точности можно считать, что практически все напряжение U, снимаемое с потенциометра R3, на емкостном делителе приложено к сегнетоэлектрическому конденсатору С1. Действительно, так как Uc1 /Uc2 = C2 /C1 >> 1, то U = Uc1 + Uc2@ Uc1. Тогда, считая электрическое поле внутри конденсатора С1 однородным, имеем:
![]() , (1.17)
, (1.17)
где Е – напряженность поля в пластине сегнетоэлектрика; h – толщина пластины.
С учетом (1.17) напряжение UX можно представить в виде:
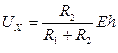 . (1.18)
. (1.18)
Таким образом, в рассмотренной электрической схеме на вертикальную и горизонтальную развёртку осциллографа одновременно подаются периодически изменяющиеся напряжения, пропорциональные, соответственно, электрическому смещению D и напряженности поля Е в исследуемом сегнетоэлектрике, в результате чего на экране осциллографа наблюдается петля гистерезиса (см. рис. 1.3).
Выражения (1.15), (1.18) позволяют найти смещение D и напряженность Е электрического поля в сегнетоэлектрике, если предварительно известны величины UY, UX , которые можно измерить с помощью осциллографа:
UY=KY y, (1.19)
UX=KX x, (1.20)
где x, y – отклонения электронного луча на экране осциллографа по осям X и Y соответственно (единицей измерения является одно деление масштабной сетки экрана); KY и KX – коэффициенты отклонения каналов Y и X осциллографа. Учитывая (1.19) и (1.20), из выражений (1.15) и (1.18) получим:
![]() , (1.21)
, (1.21)
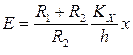 . (1.22)
. (1.22)
Применим полученные соотношения для нахождения тангенса угла диэлектрических потерь в сегнетоэлектрике и исследования зависимости e(E).
Подставляя в (1.12) выражения (1.21) и (1.22), имеем:
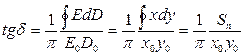 , (1.23)
, (1.23)
где Sп – площадь петли гистерезиса в координатах x, y (единица измерения – одна клетка); x0, y0 – координаты вершины петли гистерезиса.
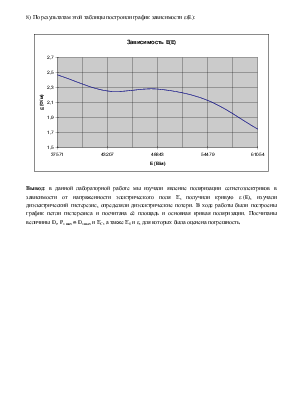
Для измерения диэлектрической проницаемости сегнетоэлектрика e используем тот факт, что основная кривая поляризации (кривая ОАВ на рис. 1.3) является геометрическим местом точек вершин циклов переполяризации, полученных при различных максимальных значениях напряженности поля в образце. Для каждой ее точки можем записать соотношение (1.5) в виде D0=ee0 Е0 , где D0, E0 – координаты вершин циклов поляризации. Тогда, определив с помощью формул (1.21) и (1.22) значения D0 и E0 вершин нескольких циклов, можно из (1.5) найти несколько значений e согласно следующему выражению и изучить зависимость e(E).
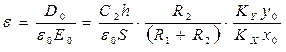 , (1.24)
, (1.24)
где S =0.25pd2– площадь обкладок конденсатора С1.
ИСПОЛЬЗУЕМЫЕ ФОРМУЛЫ
![]() (1)
(1)
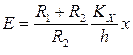 (2)
(2)
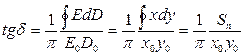 (3)
(3)
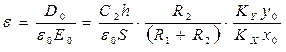 (4)
(4)
ВЫПОЛНЕНИЕ РАБОТЫ
1) Записываем координаты вершин петли, не устанавливая её в центральное положение на экране: x0 = -3 y0 = -5
x0’ = 4,5 y0’ = 8,5
Ввиду симметричности петли находим по этим значениям координаты её центра: xц = 0,75 yц = 1,75
Коэффициент отклонения КY при данных наблюдениях составлял 5, что уже было учтено при записи координат вершин и будет учтено при изображении графика в следующем пункте.
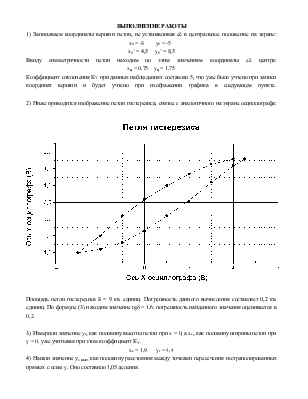
2) Ниже приводится
изображение петли гистерезиса, снятое с аналогичного на экране осциллографа:
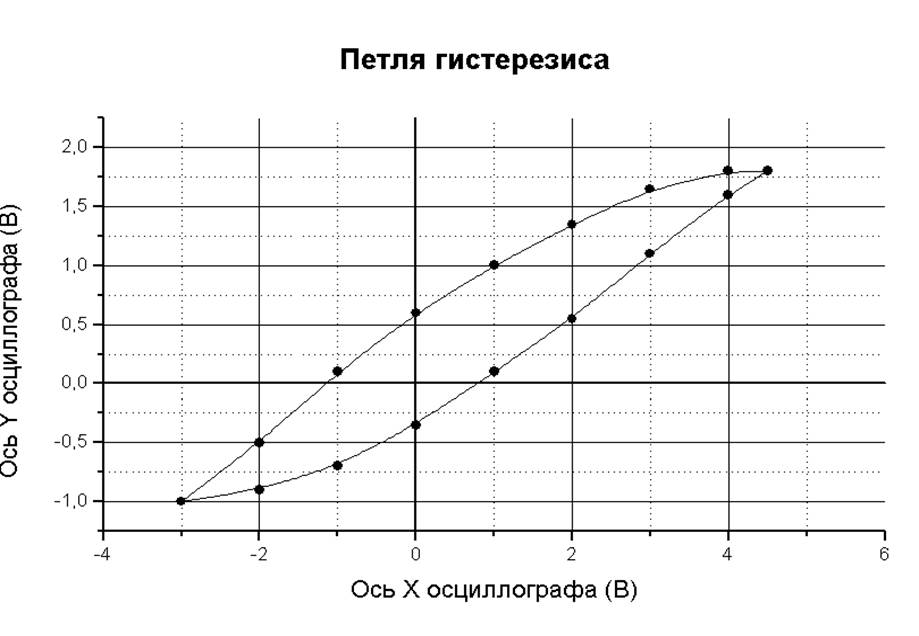
Площадь петли гистерезиса S ≈ 9 кв. единиц. Погрешность данного вычисления составляет 0,2 кв. единиц. По формуле (3) находим значение tgd = 1,6; погрешность найденного значения оценивается в 0,2.
3) Измерили значение yr, как половину высоты петли при x = 0, а xc, как половину ширины петли при y = 0, уже учитывая при этом коэффициент КY.
xc = 1,9 yr = 4,4
4) Нашли значение уs max, как половину расстояния между точками пересечения экстраполированных прямых с осью y. Оно составило 1,05 деления.
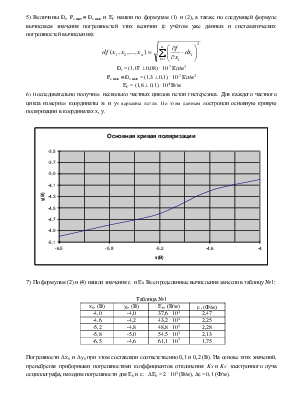
5) Величины Dr, Ps max @ Ds max и ЕC нашли по формулам (1) и (2), а также по следующей формуле вычисляем значения погрешностей этих величин (с учётом уже данных и систематических погрешностей вычисления):
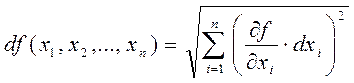
Dr = (1,07 ± 0,08) . 10-7 Кл/м2
Ps max @ Ds max = (1,3 ± 0,1) . 10-7 Кл/м2
ЕC = (1,8 ± 0,1) . 104 В/м
6) Последовательно получили несколько частных циклов петли гистерезиса. Для каждого частного цикла измерили координаты х0 и у0 вершины петли. По этим данным построили основную кривую поляризации в координатах х, у.
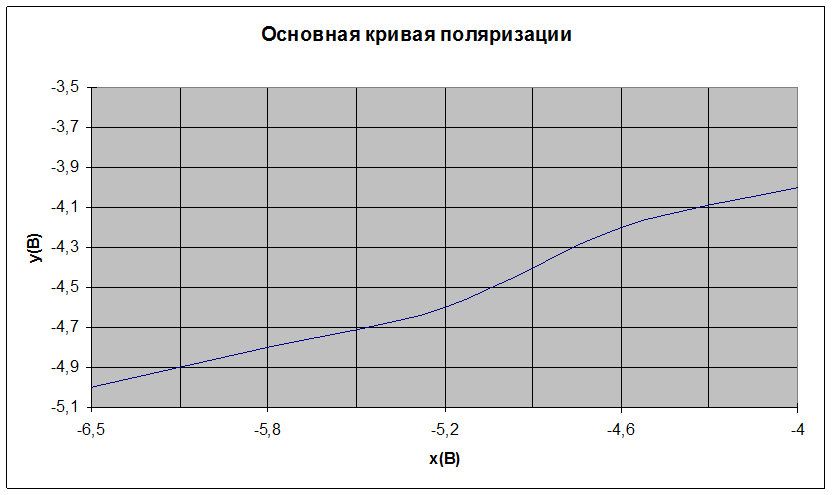
7) По формулам (2) и (4) нашли значения e и Е0. Все проделанные вычисления занесли в таблицу №1:
Таблица №1
|
х0, (В) |
y0, (В) |
Е0, (В/м) |
e, (Ф/м) |
|
-4,0 |
-4,0 |
37,6 . 103 |
2,47 |
|
-4,6 |
-4,2 |
43,2 . 103 |
2,25 |
|
-5,2 |
-4,8 |
48,8 . 103 |
2,28 |
|
-5,8 |
-5,0 |
54,5 . 103 |
2,13 |
|
-6,5 |
-4,6 |
61,1 . 103 |
1,75 |
Погрешности Dх0 и Dy0 при этом составляли соответственно 0,1 и 0,2 (В). На основе этих значений, пренебрегая приборными погрешностями коэффициентов отклонения KX и KY электронного луча осциллографа, находим погрешности для Е0 и e: DЕ0 = 2 . 103 (В/м), De = 0,1 (Ф/м).
8) По результатам этой таблицы построили график зависимости e(E):
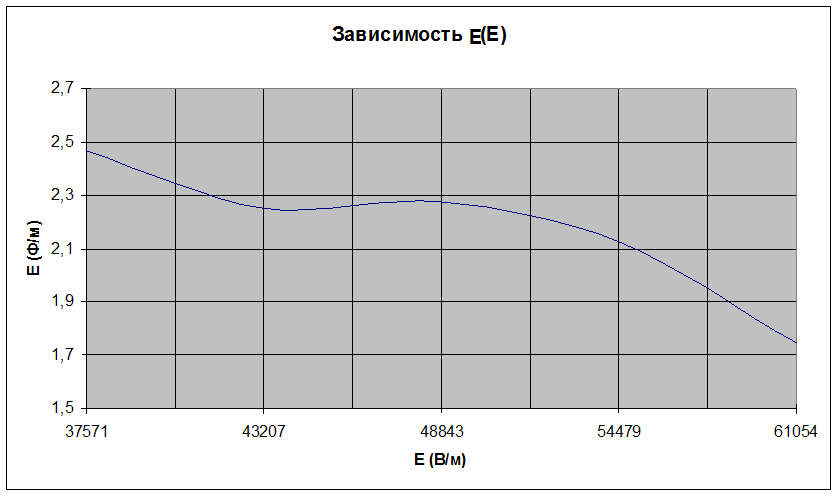
Вывод: в данной лабораторной работе мы изучали явление поляризации сегнетоэлектриков в зависимости от напряженности электрического поля Е, получили кривую e (E), изучали диэлектрический гистерезис, определяли диэлектрические потери. В ходе работы были построены график петли гистерезиса и посчитана её площадь и основная кривая поляризации. Посчитаны величины Dr, Ps max @ Ds max и ЕC, а также Е0 и e, для которых была оценена погрешность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.