Теория функций комплексной переменной и операционное исчисление

Оглавление

1  Функции  комплексной переменной. ........................................................................................ - 2 -

1.1  Множество комплексных чисел. Основные понятия и определения. ............................ - 2 - 1.2   Комплексные числа в полярной системе координат. Формула Муавра. ...................... - 3 -

1.3  Извлечение корня  n – ой  степени из комплексных чисел. ............................................. - 4 -

1.4  Множества комплексной плоскости. ................................................................................. - 5 - 1.5  Функции комплексной переменной. .................................................................................. - 6 -

1.6  Ряды в комплексной области. ............................................................................................. - 7 -

1.7  Определение основных элементарных функций. Формула Эйлера. ............................. - 9 -

1.8  Производная ФКП. Аналитические функции. Условия Коши – Римана. ................... - 11 -

1.9  Гармонические функции. ................................................................................................ - 13 -

Вопросы для самопроверки. ........................................................................................................ - 14 -

2  Интегральное исчисление функций комплексной переменной. ......................................... - 15 -

2.1  Интегралы в комплексной области. ................................................................................ - 15 - 2.4    Следствия интегральной формулы Коши. ..................................................................... - 18 - 2.5    Ряды Тейлора и Маклорена. ........................................................................................... - 19 -

2.7  Изолированные особые точки аналитической функции. ............................................... - 22 -

2.8  Бесконечно удаленная особая точка. .............................................................................. - 23 -

2.9  Вычет аналитической функции в изолированной особой точке. ................................. - 24 -

2.10  Применение вычетов к вычислению интегралов. (Основная теорема теории вычетов) . -

25 - 2.11   Вычет функции в бесконечно удаленной особой точке. ............................................. - 26 - Вопросы для самопроверки. ........................................................................................................ - 27 -

3.  Операционное исчисление. ...................................................................................................... - 28 -

3.1.  Интеграл Фурье .................................................................................................................. - 28 -

3.2.  Преобразование Лапласа и формула обращения ............................................................ - 30 -

3.3.  Основные определения операционного исчисления .................................................... - 32 -

3.4.  Основные свойства изображений и оригиналов.......................................................... - 34 -

3.5.  Основные теоремы операционного исчисления .......................................................... - 38 -

3.6.  Теоремы разложения .............................................................................................................. - 43 -

3.7.  Интегрирование линейных дифференциальных уравнений с постоянными

коэффициентами методами операционного исчисления ...................................................... - 45 -

3.8.  Изображение периодической функции ............................................................................. - 47 -

Вопросы для самопроверки. ........................................................................................................ - 49 -

Л И Т Е Р А Т У Р А.......................................................................................................................... - 50 -

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ и ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ

1  Функции  комплексной переменной.

     1.1  Множество комплексных чисел. Основные понятия и определения.

  Определение 1. Комплексным числом называется выражение z = x +iy, где  x, y ∈ℜ, а  i называется мнимой единицей и определяется следующим образом: i² = −1. Число x называется действительной частью комплексного числа: x = Re z , y – мнимой частью: y = Im z.    Два комплексных числа z₁ = x₁ + i y₁ и z₂ = x₂ + i y₂ называются равными, если их  действительные и мнимые части, соответственно, равны друг другу: z₁ = z₂ ⇔ x₁ = x₂, y₁ = y₂ . Таким образом, одно комплексное равенство эквивалентно двум действительным. Комплексное число  z = x + i y равно нулю, если  x = y = 0. 

Суммой и произведением двух комплексных чисел называются комплексные числа  def                def              z₁ + z₂ =(x₁ + x₂) + i(y₁ + y₂); z z_{1 2} =(x y_{1 1} − x y_{2    2}) + i(x y_{1 2} + x y_{2 1}) соответственно. 

Операции вычитания и деления определяются как действия обратные сложению и умножению, что приводит к следующему результату: 

                       z1 − z2 = (x1 − x2) + i⋅(y1 − y2) , zz12 = x x1 2x22 ++ y yy1 222 + i⋅ x y2 1x22 +− x yy1 222                                                                                                                                          . 

Таким образом, арифметические операции над комплексными числами производятся по обычным правилам действий с двучленами, с учетом того, что i² = −1. Отсюда следует, что операции над комплексными числами подчинены обычным законам арифметики: коммутативности, ассоциативности и т.д.  

Комплексные числа заполняют всю плоскость XOY, которую называют в этом случае комплексной плоскостью.  Множество комплексных чисел, обычно, обозначают буквой Κ. Определение 2. Число  z = x − iy называется комплексно сопряженным к  z.   

Определение 3. Величина mod z = z =    x² + y² называется модулем комплексного числа. 

Т.е. mod z  равен расстоянию  от начала координат до т. z. Нетрудно видеть, что z ² = z ⋅ z. 

 Примеры:  1) z = 32+⁻43ii ; 2) Последовательность  {i ⁿ} ={i, 1,− −i,1, , 1,i − K}.     

Замечание. На множестве комплексных чисел не определено отношение ‘больше – меньше’.

Комплексные числа можно сравнивать между собой только по модулю.

      1.2   Комплексные числа в полярной системе координат. Формула Муавра.

В предыдущем параграфе было рассмотрено представление комплексных чисел в декартовой системе координат. Рассмотрим теперь комплексные числа в полярных координатах.               Как известно, декартовы координаты выражаются через полярные следующим образом:

     y                                                                  ^_^{x = r⋅cosϕ r ≥ 0}                                  

                                                                                                  _y = r⋅sinϕ π ϕ π−   ≤  <        .

                                                                Отсюда получаем: z = r⋅(cosϕ ϕ+ isin  )  −        

                  M(x, y) = M(r, φ)                    тригонометрическая форма  комплексного числа.

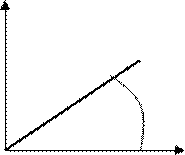                                           .                                                                                                             r                   φ                         Здесь:   

r =модуль комплексного числаz −                                         x                               (таккак cosϕ ϕ+ isin   =        cos²ϕ ϕ+ sin²  =1).

Рис. 1                                      φ – аргумент комплексного числа:  φ = arg z.

Рассматривается два стандарта изменения φ: 0≤ <^{ϕ π π ϕ π}2 и − < ≤ .  

Иногда приходится пользоваться понятием Arg z=ϕ π+ 2 n n, = 0, 1, 2,±       ± K.  

Ясно, что величина самого комплексного числа при этом никак не изменяется.          

^arctg ^y , x > 0

                                                                                                                             _         x



^arctg ^y +π, x < 0, y ≥ 0

Формулы для стандарта  -π < φ ≤ π  имеют вид: ϕ= arg z =^_        ^x                             

^arctg y −π,x < 0, y < 0

                                                                                                                                      x



                                                                                                                             приx              y              y

 (Для стандарта: 0 ≤ φ < 2π  формулы будут немного отличаться) Аргумент числа  z = 0  не определен. 

  Примеры: − 2 ; i ; 1 − i    3 .  {2, π ; 1, π/2 ; 2, −π/3 или 5π/3 } 

Рассмотрим произведение 2-х комплексных чисел: z1z2 = r1 r2(cosϕ₁ + isinϕ₁ )(cosϕ₂ + isinϕ₂ ) = = rr_{1 2}(cosϕ ϕ₁ cos ₂ −sinϕ ϕ₁ sin ₂ + i(sinϕ ϕ₁ cos ₂ + sinϕ ϕ₂ cos ₁)) = rr_{1 2}(cos(ϕ ϕ₁ + ₂) + isin(ϕ ϕ₁ + ₂)).

Т.е. модуль произведения комплексных чисел равен произведению их модулей, а аргумент – сумме аргументов. Отсюда следует формула Муавра:

                                                (cosϕ ϕ+ isin  )ⁿ = cosnϕ+ isinnϕ .            

      1.3  Извлечение корня  n – ой  степени из комплексных чисел.

n

По определению:( ^{n c}) = c. На множестве действительных чисел для однозначности вводится понятие