Современные представления о теплообмене и температурах, возникающих в процессе резания

Современные представления о теплообмене и температурах, возникающих в процессе резания[I1] 

Многолетние исследования тепловых процессов при резании металлов позволили установить их основные закономерности, но в то же время все еще не достигнуто полное понимание этих процессов.

В настоящее время общепринятой считается схема теплообмена, представленная А. Н. Резниковым [32]. Здесь температура в любой точке системы резания есть результат воздействия трех источников тепла: теплоты трения на участке контакта «резец-стружка», теплоты деформации и теплоты тре­ния на участке контакта «резец-заготовка».

В процессе обработки в системе заготовка–стружка–инструмент возникают следующие источники теплоты: источник трения на передней поверхности инструмента интенсивностью  и действующий на площадке контакта длиной ; источник трения на задней поверхности инструмента распределенный интенсивностью  и действующий на площадке контакта длиной ; источник теплоты, вызванный деформациями в зоне резания интенсивностью . Теплообмен между стружкой и инструментом, заготовкой и инструментом, стружкой и заготовкой происходит посредством итоговых потоков теплообмена, соответственно, , , . При наличии внешнего охлаждения, например,  в результате применения СОТС, возникает еще один сток теплоты действующий на всех свободных поверхностях заготовки, стружки и инструмента , подчиняющийся закону Ньютона-Рихмана [32].

Все перечисленные теплообразующие источники являются трехмерными, однако часто при теплофизическом анализе их полагают двумерными. В соответствии с принципами механики распределение их плотности соответствует распределению напряжений в зоне деформации и трения на контактных поверхностях (см. раздел 0):

; ; ,                                  ( 3.45)

где  и  - коэффициенты, показывающие долю механической энергии, выделяющуюся в виде теплоты соответственно при деформировании и трении. Значения этих коэффициентов в работах различных авторов весьма противоречивы. Так, например, А. Н. Резников [32] принимает эти коэффициенты равными 1 во всех случаях, в то время как некоторые западные ученые [94] принимаю эти коэффициенты равными соответственно 0.9 и 0.5 в условиях обработки углеродистой стали быстрорежущим инструментом.

Однако часто при расчете температур аналитическими методами принимают  равнораспределенным по плоскости сдвига,  распределенным по смешенному закону, а  по несимметричному нормальному закону.

Общую мощность тепловыделения предполагают эквивалентной всей механической работе деформирования материала в зонах А, Б, В (см. рисунок 3.2) и работе сил трения на контактных площадках инструмента[DV2] . Таким образом суммарная мощность тепловыделения равна [32]:

,                                           ( 3.46)

где , ,  - соответственно мощности тепловыделения источников, возникающих как результат перехода в теплоту работы деформирования, работы сил трения на передней и задней поверхностях режущего клина:

, ,

Из теплофизики известно, что теплопередача в системе резания подчиняется уравнению теплопроводности [3]:

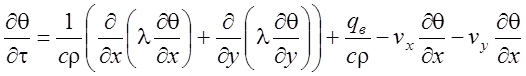,                ( 3.47)

где  - коэффициент теплопроводности, в общем случае зависящий от температуры, Вт/(м×°С); с - удельная теплоемкость, Дж/(кг×°С);  - плотность материала, кг/м³;  - объемная плотность тепловыделения внутренних источников, Дж/м³;  - время, с;  - температура, °С; , - проекции на оси координат скорости частиц среды, м/с.

Существует несколько методов аналитического определения температур, каждый из которых в своем аналитическом описании основывается на тех или иных допущениях и предпосылках. Наиболее интересные и важные теоретические исследования в области теплофизики резания (с позиции рассматриваемой задачи) выполнены коллективами и отдельными учеными: А. Н. Резниковым, В. А. Остафьевым, С. С. Силиным, Н. В. Талантовым, М. Г. Стивенсоном и др.

Наиболее широко распространен метод стационарных и движущихся источников тепла, для аналитического исследования температурных полей на контактных поверхностях «резец-стружка» и «резец-заготовка», разработанный А. Н. Резниковым, С. С. Силиным и др. [49, 32, [i]].

Метод предполагает целый ряд допущений:

упрощенная геометрическая форма режущей части инструмента, стружки и заготовки;

принятые упрощенные законы распределения тепловых источников, что дает более интенсивный рост температур в плоскости сдвига [3]

практически не учитываются зависимости свойств материала от температуры и др.

Кроме того, этот метод не позволяет непосредственно рассчитать темпера­турное поле в системе резания и, следовательно, является недостаточно эффективным для решения задачи о термические напряжениях.

Более полное решение уравнения теплопроводности может быть выполнено методом конечных элементов (МКЭ), который позволяет не только получить более подробную информацию о температурном поле, более корректно и гибко задать граничные условия и не прибегать к геометрическому упрощению задачи, но и выполнить расчеты с учетом зависимости теплофизических свойств материалов системы от температуры, эффективно решать задачу конвективного теплообмена и т.д. Интересной особенностью является возможность гибко задать распределение тепловых источников по сколь угодно сложному закону или непосредственно вычислить его при моделировании стружкообразования из расчета напряженно-деформированного состояния (НДС) срезаемого слоя. В решении таких задач методом конечных элементом уже достигнут определенный прогресс [1].

При рассмотрении свободного прямоугольного резания указанная задача сводится к интегрированию дифференциального уравнения теплопроводности по площади сечения заготовки, стружки и инструмента главной секущей плоскостью при заданных начальных и граничных условиях:

Исследования теплофизики резания показали, что тепло, образующееся при резании, переходит в стружку, заготовку и инструмент. Было установлено, что теплоотвод в инструмент минимален при любых условиях обработки, что вызвано, прежде всего, низкой теплопроводностью инструментальных материалов по сравнению с обрабатываемыми [11].

Контактные температуры могут достигать температуры плавления обрабатываемого материала, и в несколько раз превосходить среднюю температуру стружки. Их распределение приведено на рис[DV3] . А. Н. Резников отмечает, что теплоотвод через заднюю поверхность может быть достаточно сильным и в этом случае заготовка может служить своеобразным охладителем инструмента, причем достаточно активным [32].

Приводимые в литературе распределения температуры в РЧИ свидетельствуют о наличии довольно высоких градиентов ее изменения, что несомненно вызывает температурные напряжения в инструменте[3].