




Математическая модель упругопластической деформации КЭ
Считается экспериментально доказанным факт, что уширение стружки при прямоугольном резании мало (т. е. деформация стремится к нулю). Основываясь на этом факте принята гипотеза о плоской деформации, т. е.
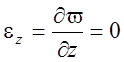 ,
, 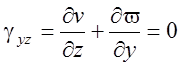 ,
,
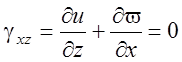 ,
, ![]() . (
4.8)
. (
4.8)
Кроме этого примем следующие допущения:
– рассматривается первый этап внедрения инструмента в заготовку и изучается образование следующего элемента стружки в предположении, что силы остаются постоянными в пределах деформирования; геометрия срезаемого слоя определяется по данным эксперимента и расчетным формулам, при веденным ниже.
– материал заготовки описывается упругопластической моделью с линейным упрочнением (см. раздел 3); его реологическая модель задается соотношением:
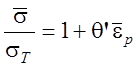 , (
4.9)
, (
4.9)
где ![]() -
приведенный модуль упрочнения и
-
приведенный модуль упрочнения и ![]() определяются
экспериментально;
определяются
экспериментально;
– материал заготовки однороден и изотропен, отсутствуют дефекты и случайные отклонения свойств;
– процесс резания считается адиабатическим;
– предполагается, что отсутствует наростообразование;
– в первом приближении принято, что трение подчиняется закону Кулона-Амонтона (3.28), при чем коэффициенты трения на передней и задней поверхностях считаются различными и определяются из эксперимента для данной пары обрабатываемый - инструментальный материал (см. раздел 5).
Уравнение равновесия (3.55) для упруго-пластического материала с линейным упрочнением в Лагранжиевой формулировке может быть представлено в виде [85]:
![]() , (
4.10)
, (
4.10)
где 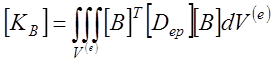 -
матрица жесткости;
-
матрица жесткости; ![]() - матрица
дифференцирования перемещений;
- матрица
дифференцирования перемещений; ![]() - матрица
материала;
- матрица
материала; 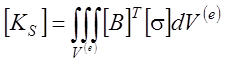 [DV1] -
т.н. инкрементальная геометрическая матрица жесткости;
[DV1] -
т.н. инкрементальная геометрическая матрица жесткости; ![]() -
вектор вариаций инкрементальных перемещений;
-
вектор вариаций инкрементальных перемещений; 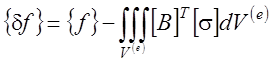 -
вектор несбалансированных сил;
-
вектор несбалансированных сил; ![]() - вектор внешних
узловых сил.
- вектор внешних
узловых сил.
Матрица дифференцирования в полярных координатах может быть записана в виде:
![]() , (
4.11)
, (
4.11)
где 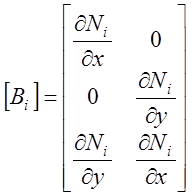 -
блок, соответствующий узлу i.
-
блок, соответствующий узлу i.
Производные функции формы по глобальным координатам можно получить, используя матрицу Якоби:
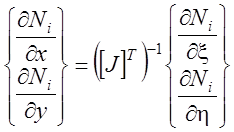 ,
,
где 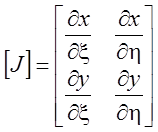 -
матрица Якоби, компоненты которой могут быть определены посредством
дифференцирования выражения (4.3).
-
матрица Якоби, компоненты которой могут быть определены посредством
дифференцирования выражения (4.3).
Предположим, что изменение деформации при бесконечно малом приращении напряжения может быть представлено в виде суммы упругой и пластической частей (см. 3.48) и в случае КЭ формулировки записано в виде:
![]() , (
4.12)
, (
4.12)
где ![]() -
вектор деформаций в общем случае плоской деформации
-
вектор деформаций в общем случае плоской деформации
Из теории упругости хорошо известно, что упругие
приращения деформации связаны с приращениями напряжения симметричной матрицей ![]() . Учитывая ассоциированный закон
пластичности (3.51) выражение (4.12) можно записать:
. Учитывая ассоциированный закон
пластичности (3.51) выражение (4.12) можно записать:
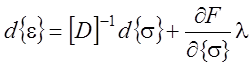 . (
4.13)
. (
4.13)
Выполняя некоторые преобразования [82] получаем выражение,. в явном виде определяющее изменение напряжений через изменение деформаций:
![]() , (
4.14)
, (
4.14)
где
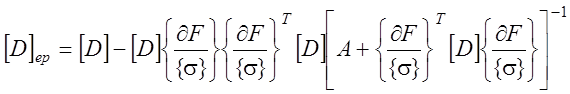 , ( 4.15)
, ( 4.15)
где ![]() -
матрица упругости ;
-
матрица упругости ;
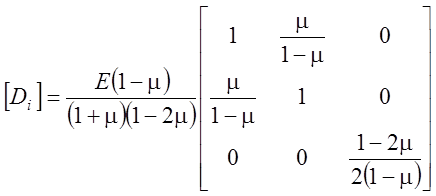 .
.
Принимаем в рассматриваемой модели частный случай поверхности текучести Мизеса в виде [79]:
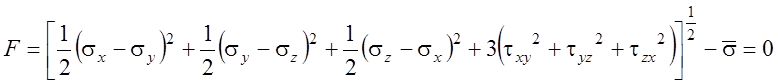 ( 4.16)
( 4.16)
В этом случае с учетом принятой реологической модели (4.9) обрабатываемого материала параметр ![]() в
выражении (4.15) равен модулю упрочнения
в
выражении (4.15) равен модулю упрочнения ![]() .
В этом случае модуль упрочнения определяется экспериментально из опыта на
одноосное растяжение.
.
В этом случае модуль упрочнения определяется экспериментально из опыта на
одноосное растяжение.
Вектор внешних узловых сил может быть определен по формуле:
![]() , (
4.17)
, (
4.17)
где ![]() -
вектор внешних сосредоточенных сил;
-
вектор внешних сосредоточенных сил; 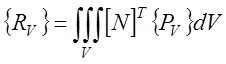 - вектор приведенных
к узлам объемных сил;
- вектор приведенных
к узлам объемных сил;  - вектор
приведенных к узлам поверхностных сил;
- вектор
приведенных к узлам поверхностных сил; 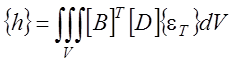 -
фиктивная узловая температурная нагрузка, определяемая из расчета температурных
полей (раздел 4.2.2).
-
фиктивная узловая температурная нагрузка, определяемая из расчета температурных
полей (раздел 4.2.2).
Таким образом, имея матрицы жесткости и вектора нагрузок
для каждого КЭ составляет суммарную матрицу жесткости с учетом граничных
условий (см. раздел 3). Граничные условия приняты в виде жесткого защемления
заготовки по границе ABCD[DV2] .
Влияние такого рода граничных условий на НДС в зоне стружкообразования
незначительно, поскольку исследуемая область значительно больше этой зоны.
Инструмент имеет жесткую границу 123[DV3]
и его вращение вокруг оси ![]() ограничено. На
границе контакта инструмента с заготовкой и стружкой введены т.н. контактные
элементы с заданным коэффициентом трения., определяемым экспериментально по
методике, изложенной в разделе 5. Условие наличия контакта между «ведущим» и
«ведомым» элементами можно записать в виде:
ограничено. На
границе контакта инструмента с заготовкой и стружкой введены т.н. контактные
элементы с заданным коэффициентом трения., определяемым экспериментально по
методике, изложенной в разделе 5. Условие наличия контакта между «ведущим» и
«ведомым» элементами можно записать в виде:
![]() ,
,
где ![]() -
нормальная нагрузка в контакте со стороны «ведомой» поверхности;
-
нормальная нагрузка в контакте со стороны «ведомой» поверхности; ![]() - нормаль к «ведущей» поверхности.
- нормаль к «ведущей» поверхности.
Нагрузка в данной модели прикладывалась в виде
приведенных компонент силы резания к жесткой границе 1-2 инструмента.
Составляющие ![]() и
и ![]() рассчитывались
по формуле (5.1) и компонента Px принимается равной 0.
рассчитывались
по формуле (5.1) и компонента Px принимается равной 0.
В виду того, что на участках проскальзывания резания не происходит, то результаты расчета на этих участках по приведенной методике не имеют физического смысла (см. раздел 2).
Стр: 1
[DV1]Уточнить формулу
Стр: 1
[DV2]Уточнить по рисунку
граничные условия
Стр: 1
[DV3]Уточнить по рис.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.