Предел последовательности. Вычисление значения предела. Признаки сходимости знакопостоянных рядов. Вычисление суммы и произведения элементов ряда

Лабораторная работа №2

Тема: Пределы. Ряды. (4 часа)

Цель работы: Освоить основные операции вычисления пределов  и  обработки рядов.

Содержание

1. Предел последовательности_ 1

1.1. Теоремы о пределах последовательности_ 1

2. Предел функции_ 2

2.1.Односторонние пределы_ 2

3. Вычисление значения предела 2

Пример 1_ 2

Пример 2_ 2

Пример 3_ 2

4. Ряды_ 3

Признаки сходимости знакопостоянных рядов 3

Вычисление суммы и произведения элементов ряда 3

5. Вычисление суммы и произведений элементов рядов с учетом условия 3

Условная функция IF_ 3

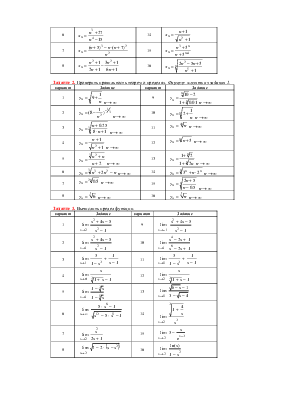
Индивидуальные задани_ 5я

Задание 1. 5

Задание 2_ 5

Задание 3_ 6

Задание 4_ 7

Задание 5_ 7

Задание 6_ 7

Задание 7_ 7

Задание 8. 7

Контрольные вопросы_ 8

1. Предел последовательности

Говорят, что последовательность x₁, x₂, …, x_n имеет своим пределом число a (сходится к а), то есть

, если для любого ε>0 существует число N=N(ε) такое, что

.

В частности, x_n называется бесконечно малой, если

Последовательность, не имеющая предела, называется расходящейся.

1.1. Теоремы о пределах последовательности

-  - 

-  - 

-  - 

2. Предел функции

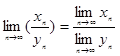
Число а называется пределом функции f(x) в точке x₀, если для любой последовательности {x_n}, x_n€(α;β), x_n≠x₀, сходящийся к x_0, последовательность {f(x_n)} сходится к а:

Функция f(x) называется бесконечно большой при , если .

Функция f(x) называется бесконечно малой при , если .

2.1.Односторонние пределы

Пусть область определения функции f(x) содержит интервал (α; x₀).

Число а называется пределом слева функции f(x) в точке x₀ (или при  ), если для каждого числа ε>0 существует такое число δ>0, что для всех x, удовлетворяющих неравенствам x₀< δ<x<x₀, выполняется неравенство .

Предел слева функции f(x) в точке x₀≠0 обозначают:

_.

Предел слева функции f(x) в точке x₀=0 обозначают:

.

Аналогично, в случае, когда область определения функции f(x) содержит интервал (x₀;β), вводится понятие предела справа.

Предел справа функции f(x) в точке x₀≠0 обозначают:

_.

Предел справа функции f(x) в точке x₀=0 обозначают:

.

Вычисление односторонних пределов в MathCad производится по соответствующим шаблонам:

3. Вычисление значения предела

Вычисление значения предела выполняется по следующему алгоритму:

1.  1.Выбрать подходящий шаблон на соответствующей панели инструментов и заполнить его конкретными данными;

2.  2.Нажать на клавиатуре Ctrl+.(точка);

3.  3.Нажать на клавиатуре Enter.

Пример 1. Найти , если

Пример 2. Найти предел функции .

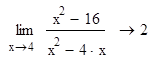
Пример 3. Вычислить односторонние пределы слева и справа от точки x=0

4. Ряды

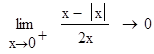
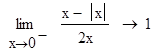
Числовой ряд

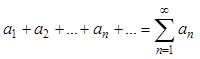
называется сходящимся, если существует конечный предел , где . В противном случае ряд называется расходящимся.

Признаки сходимости знакопостоянных рядов:

Признак Коши.

Если a_n≥0 и , то при q<1 ряд сходится, а при q≥1 расходится.

Признак Даламбера.

Если a_n>0 и 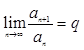, то при q<1 ряд сходится, а при q≥1 расходится.

Вычисление суммы и произведения элементов ряда

Вычисление производится при помощи соответствующих шаблонов:

5. Вычисление суммы и произведений элементов рядов с учетом условия

Условная функция IF

Синтаксис:

Правило вычисления условной функции if:

Если логическое выражение равно 1 (истина), то функция принимает значение равное значению арифметического выражения 1 ; если логическое выражение равно 0 (ложь), то функция принимает значение равное значению арифметического выражения 2.

Применение: Условная функция используется в арифметических выражениях, стоящих в правой части локального оператора присваивания.

2.2. Логические операции

1.  1.  Логическая операция ИЛИ (логическое сложение, объединение). Обозначается знаком ν и записывается в виде:

<логическое выражение 1> ν <логическое выражение 2>

Результат операции равен 0, если оба логических выражения равны 0 и равен 1 для всех остальных значений логических выражений.

2.  2.  Логическая операция И(логическое умножение, пересечение). Обозначается знаком Λ и записывается в виде:

<логическое выражение 1 > Λ < логическое выражение 2>

Результат равен 1, если оба логических выражения равны 1 и равен 0 для всех остальных значений логических выражений.

3.  3.  Логическая операция НЕ(логическое отрицание). Вводится знаком [¬] и записывается в виде:

¬<логическое выражение>

Результат равен 1, если логическое выражение равно 0 и наоборот.

Примечания:

§  §  операция ИЛИ может также обозначаться знаком [+], а И – знаком [*]

§  §  для ввода знаков отношений и логических операций  используется панель Boolean и клавиатура:

2.3. Логическое выражение

Логическим выражением называется конструкция, составленная из выражений-отношений, логических операций и круглых скобок. Значение логического выражения вычисляется слева направо с учетом известного правила о приоритете операций.

Список приоритетов (по их убыванию):

-  -круглые скобки;

-  -логическая операция И;

-  -логическая операция ИЛИ.

Пример 1. Найти сумму положительных (больших 0) из 10 первых элементов знакопеременного ряда   

Пояснение: данное условие можно реализовать с помощью функции проверки условия if,  а именно при переборе для суммирования всех элементов ряда проверяется условие M_i>0, в том случае, когда это условие выполняется, суммируется М_i элемент ряда, в противном случае к сумме добавляется 0.

Пример 2. Найти произведение положительных (больших 0) из 10 первых элементов знакопеременного ряда   

Пояснение: данное условие можно реализовать с помощью функции