










Лабораторная работа № 6. Дифференциальное исчисление в пакете MathCad.
цель работы: освоение основных приемов вычисление производных высших порядков в пакете MathCad (4 часа)
Содержание
1. Определение и понятие производной
2. Средства дифференцирования в MathCad
2.1 Примеры нахождения производных
3. Нахождение производной в общем виде
4. Физический смысл производной
4.1 Пример применения физического смысла производной
5. Геометрический смысл производной
5.1 Пример нахождения уравнения касательной функции в некоторой точке
6. Приложения производной
6.1. Экстремумы функции
6.2. Разложение функции в ряд Тейлора.
7. Встроенные функции решения краевых задач, заданных в форме Коши
7.2 Функция Odesolve()
7.2 Функция Rkfixed()
Порядок выполнения работы
Задание 1. Построение касательной к функции в точке
Задание 2. Физический смысл производной.
Задание 3. Определение экстремумов функции
Задание 4. Разложение функции в ряд Тейлора
Задание 5. Решение задачи Коши
Контрольные вопросы
Производной ![]() функции в точке
функции в точке ![]() называется
предел отношения приращения функции к приращению аргумента при стремлении
приращения аргумента к нулю т.е.
называется
предел отношения приращения функции к приращению аргумента при стремлении
приращения аргумента к нулю т.е. 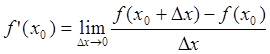
Оператор производной предназначен для нахождения значения производной функции в заданной точке.
Вызвать оператор производной можно следующими способами:
|
Используя ПИ производных и интегралов |
Используя клавиатуру |
|
|
|
для нахождения производной 1-го порядка |
Shift + ? |
|
|
для нахождения производной n-го порядка |
Ctrl + Shift + ? |
Для нахождения производной нужно:
1. 1. Определить точку (или диапазон), в которой будет найдена производная;
2. 2. Вызвать оператор нахождения производной:
v v появится шаблон нахождения производной 1-го порядка
![]()
или
v v шаблон нахождения производной n-го порядка
![]()
3. 3. Заполнить шаблон данными:
1. Найти производную функции ![]() в
точке x=2.
в
точке x=2.
![]()
![]()
2. Найти производную той же самой функции в точках x, на заданном интервале.

3.Найти вторую производную той же функции в точке x=3.5
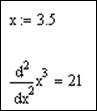
Для вывода на экран формулы нахождения производной необходимо:
v v на ПИ выбрать шаблон неопределенного интеграла производной;
v v заполнить его;
v v набрать на клавиатуре Ctrl+.(точка);
v v нажать ввод.
Пусть s=s(t) представляет закон прямолинейного движения материальной точки. Это уравнение выражает путь s, пройденный точкой, как функцию времени t. Обозначим через ∆s путь, пройденный за промежуток времени ∆tот момента t до t+∆t, то есть ∆s=s(t+∆t)-s(t).
Отношение ![]() называется
средней скоростью точки за время от t до
t+∆t.
называется
средней скоростью точки за время от t до
t+∆t.
Мгновенной скоростью точки в данный момент времени t
называется предел средней скорости за промежуток от t до
t+∆t, когда ![]() :
:
![]() или
или ![]()
Ускорение точки в данный момент вычисляется по следующей формуле:
![]()
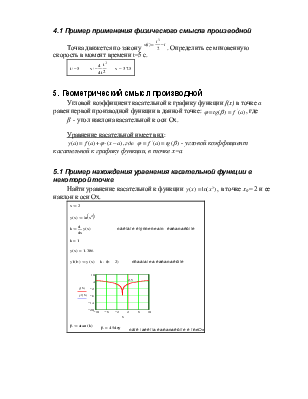
Точка движется по закону ![]() .
Определить ее мгновенную скорость в момент времени t=5 с.
.
Определить ее мгновенную скорость в момент времени t=5 с.
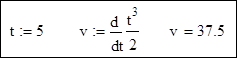
Угловой коэффициент касательной к графику функции f(x) в точке a равен первой
производной функции в данной точке: ![]() , где
, где
β - угол наклона касательной к оси Ох.
Уравнение касательной имеет вид:
![]() - угловой коэффициент касательной к графику
функции, в точке x=a
- угловой коэффициент касательной к графику
функции, в точке x=a
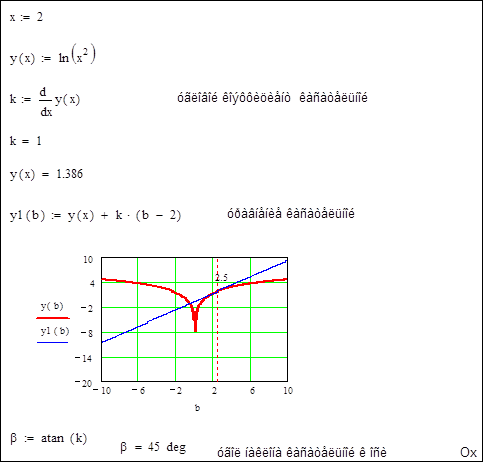
Найти уравнение касательной к функции ![]() , в точке x0 = 2 и ее
наклон к оси Ох.
, в точке x0 = 2 и ее
наклон к оси Ох.
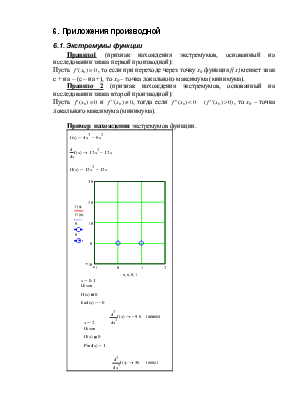
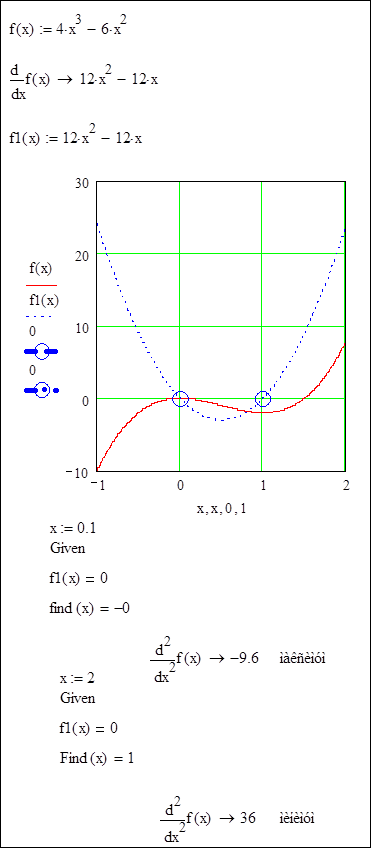
Правило1 (признак нахождения экстремумов, основанный на исследовании знака первой производной):
Пусть ![]() , то если при
переходе через точку x0 функция f(x) меняет знак с + на – (с – на +), то x0 – точка
локального максимума (минимума).
, то если при
переходе через точку x0 функция f(x) меняет знак с + на – (с – на +), то x0 – точка
локального максимума (минимума).
Правило 2 (признак нахождения экстремумов, основанный на исследовании знака второй производной):
Пусть ![]() и
и ![]() , тогда если
, тогда если ![]() , то x0 –
точка локального максимума (минимума).
, то x0 –
точка локального максимума (минимума).
Пример нахождения экстремумов функции.
Для приближенного определения значения функции f(x) разложим данную функцию в Ряд Тейлора в окрестности точки x=a.
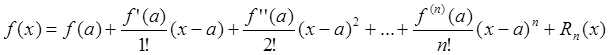
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.