Для нахождения второго уравнения, связывающего коэффициенты A1 и A2, найдем напряжение на индуктивности UL (t):
, (6)
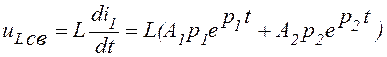. (7)
В установившемся режиме, смотри 2.1.3, напряжение на индуктивности
UL = 0, таким образом, принужденная составляющая ULпр = 0. Подставив выражение (7) и ULпр = 0 в выражение (6) получим:
. (8)
Из качественного анализа, смотри 2.1.2, нам известно, что UL(0+) = 0. Тогда из выражения (8) следует, что
= 0.
Таким образом, получаем второе
уравнение системы 
или
. (9)
Уравнения (5) и (9) образуют систему, решив которую найдем A1 и A2 :
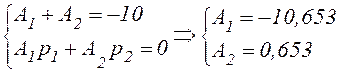
Подставляя значения р1 и р2 , А1 и А2 в выражения (4) и (8),получаем:
,
.
Покажем методику определения токов в других ветвях и напряжения на конденсаторе.
2.2.3 Определение i2(t) и uc(t).
Ток
i2(t) = i2св + i2пр (10)
где i2св - свободная составляющая переходного тока;
i2пр - принужденная составляющая переходного тока.
Так как характеристическое уравнение (3) имеет два вещественных корня, то свободная составляющая тока i2 определяется выражением:
. (11)
Вследствие того, что постоянный ток через конденсатор не проходит, принужденная составляющая, смотри 2.1.3, равна: i2пр = 0.
Чтобы определить свободную составляющую тока i2св, необходимо составить систему двух уравнений, связывающих постоянные A1 и A2 .
Из качественного анализа, в соответствии с 2.1.2, нам известно значение тока i2 непосредственно после коммутации: i2(0+) = -30А.
Используя выражения (10) и (11),получим первое уравнение, связывающие коэффициенты A1 и A2:
А1 + А2 = -30. (12)
Для нахождения второго уравнения, связывающего коэффициенты A1 и A2, найдем uс (t):
, (13)
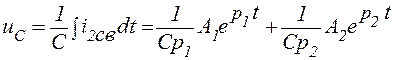. (14)
Ввиду того, что после коммутации
в установившемся режиме (п.2.1.3) напряжение uC= 50В, принужденная составляющая напряжения на конденсаторе
=50В.
В соответствии с 2.1.2, нам
известно, что напряжение на конденсаторе непосредственно после коммутации 
(0+) =150В.
Подставив эти значения и выражение (14) в (13), получим второе уравнение, связывающие коэффициенты A1 и A2:
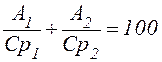. (15)
Из уравнений (12) и (15) составляем систему, решив которую, найдем постоянные интегрирования A1 и A2:
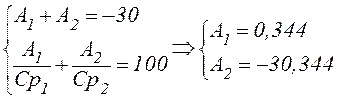
Подставляя значения р1 и р2 , А1и А2 в выражение для i2(t)и 
, получаем:
А,
В.
2.2.4 Определение i3(t)
Ток i3(t) в общем виде равен:
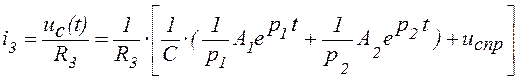. (16)
Подставив значения параметров в выражение (16), окончательно получим:
.
2.3 Расчет переходного процесса в цепи операторным методом
Расчет состоит из двух этапов:
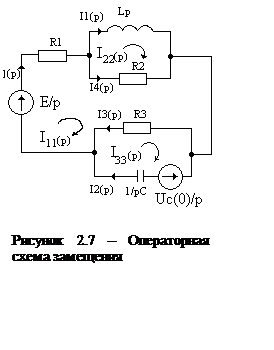Первый этап: составление операторной схемы
замещения послекоммутационной схемы, изображенной на рисунке 2.7 и определение
операторного изображения искомой функции.
Второй этап: переход от изображения функции к ее оригиналу.
Первый этап. При составлении операторной
схемы, смотри рисунок 2.7, все переменные во времени величины заменяются их
операторными изображениями. Катушка заменяется последовательно соединенным
операторным сопротивлением Lpи источником напряжения Li1(0), где i1(0)- значение тока в индуктивности при t=0+. Конденсатор заменяется последовательно
соединенными операторным сопротивлением 
и источником напряжения uc(0)/р, где uc(0)- значение напряжения на емкости
при t=0+. Направление источника Li1(0) совпадает с направлением тока ветви, а
направление источника uc(0)/р противоположно току в этой ветви.
В схеме, изображенной на рисунке 2.3, начальные условия имеют следующие значения: i1(0+) = 0 , uc(0+) = 150В. Поэтому источник напряжения Li1(0) на операторной схеме замещения не показан.
Искомый ток I1(p) для схемы замещения, изображенной на рисунке 2.7, можно найти с помощью метода контурных токов. Он будет равен контурному току I22(p).
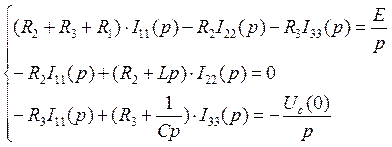7)
Решив систему (17), найдем ток I22(p):
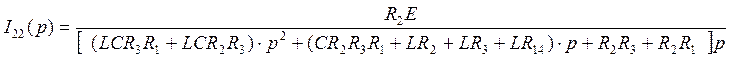. (18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.