Качественный анализ переходных процессов. Расчет переходного процесса классическим и оперативным методом, страница 2

- используя операторный метод расчета, определить закон изменения во времени той же величины, что в пункте 2;

- построить графики искомых функций в интервал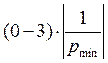е , где - наименьший по модулю корень характеристического уравнения.

2 ТИПОВАЯ ЗАДАЧА ПО РАСЧЕТУ ПЕРЕХОДНОГО ПРОЦЕССА

Произведем расчет переходного процесса в цепи, изображенной на рисунке 2.1:

Параметры цепи:

E	=	150В;
C	=	5 мкФ;
L	=	2 мГн;
R1	=	10 Ом;
R2	=	10 Ом;
R3	=	5 Ом;
i1	-	?

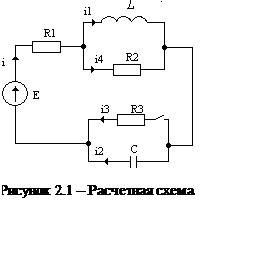
2.1Качественный анализ переходных процессов

2.1.1 Расчет токов и напряжений до коммутации (t=0-)

Так как сопротивление конденсатора (идеального) постоянному току стремится к бесконечности (), а катушка индуктивности (идеальная) не представляет сопротивления постоянному току (R = 0), то докоммутационная схема будет выглядеть следующим образом (рисунок 2.2):

I₁(0_-) = i₂(0_-) = i₃(0_-) = i₄(0_-) = i(0_-)= 0А, U_c(0_-) = E=150В, U_L(0_-) = 0В.

2.1.2 Расчет токов и напряжений непосредственно после коммутации (t=0₊)

Коммутационная схема приведена на рисунке 2.3.

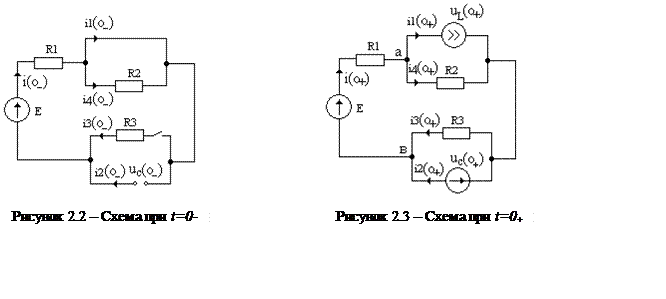
В соответствии с первым законом коммутации

i₁(0+) = i₁(0-) = 0.

В соответствии со вторым законом коммутации

Uc(0+) = Uc(0-) = 150В.

Для узла «а»: i(0+) = i₁(0+)+ i₄(0+),так как i₁(0+) = 0, то i(0+) = i₄(0+).

i(0+)(R₁+ R₂) = Е - Uc (0+),

i(0+) = (Е - Uc (0+))/( R₁+ R₂)= (150-150)/10+10= 0,

i₄(0+)= i(0+)=0 А,

Uc(0+)=i₃(0+)R₃=> i₃(0+)=Uc(0+)/R₃=150/5= 30А.

Для узла «в»:

i₂(0+)+i₃(0+)-i(0+) =0 => i₂(0+)= i(0+) - i₃(0+) =0 – 30= - 30А,

U_L(0+) – i₄(0+)R₂ = 0В, U_L(0+) = i₄(0+)R₂ =0В.

Таким образом, получили следующие значения токов и напряжений:

i₁(0+) = 0А, i₂(0+) = -30А, i₃(0+)=30А,

i₄(0+) = i(0+) = 0А, Uc(0+) = 150В, U_L(0+) = 0В.

2.1.3 Расчет токов и напряжений в установившемся режиме

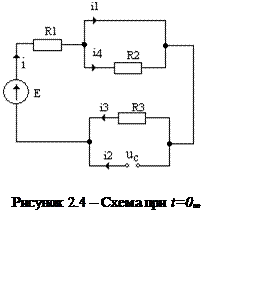
Схема установившегося режима приведена на рисунке 2.4.

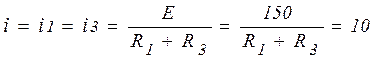А,

i₂= i₄= 0, U_L= 0В, Uc = i₃ R₃ = 10 ^.5 = 50В.

2.1.4 Построение графиков переходного процесса

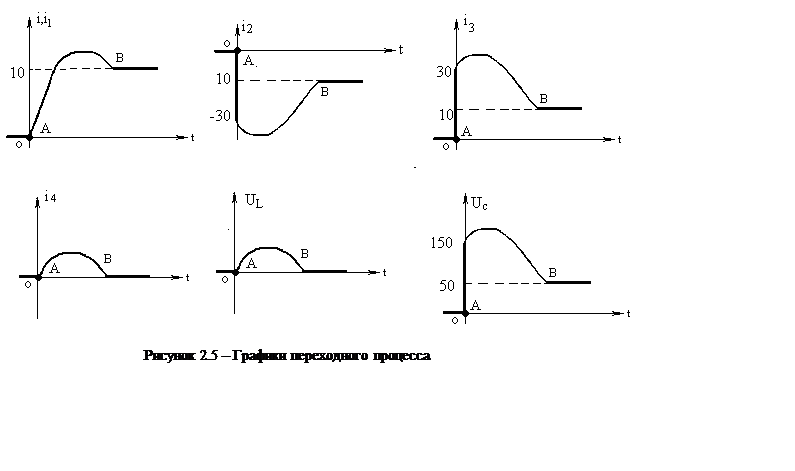
Графики изменения токов во всех ветвях схемы и напряжений на реактивных элементах схемы представлены на рисунке 2.5:

Точка А соответствует значениям переменных в момент коммутации (t = =0), смотри 2.1.2. Точка В и, проходящие через нее прямые, соответствуют установившимся значениям переменных (t = ∞), смотри 2.1.3. Линии АВ проведены приблизительно, исходя из предположения, что во время переходного процесса токи и напряжения принимают большие значения, чем в установившемся процессе.

2.2 Расчет переходного процесса классическим методом

2.2.1 Составление характеристического уравнения

Составим выражение для входного сопротивления переменному току  между точками a и b в послекоммутационной схеме, изображенной на рисунке 2.6.

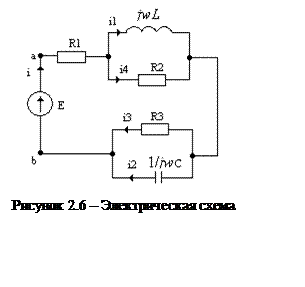
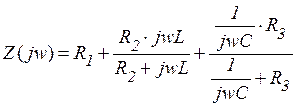                       (1)

В выражении (1) заменим p на jw, получим:

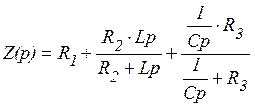                                (2)

После преобразования и приравнивания к нулю числителя выражения (2) получим характеристическое уравнение:

            (3)

Подставим в характеристическое уравнение (3) численные значения параметров:

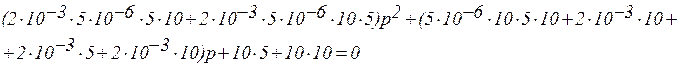
Решая данное уравнение относительно p, находим корни:

 с^-1.

2.2.2 Определение i1(t)

Ток

i₁(t) = i₁св + i₁пр, где i₁св - свободная составляющая переходного тока;

i₁пр – принужденная составляющая переходного тока.

Так как характеристическое уравнение имеет два вещественных корня, то свободная составляющая тока i1 определяется выражением:

.

В установившемся режиме (при t = ∞) через индуктивность течет ток

i1 = 10A , смотри 2.1.3, то есть принужденная составляющая тока i₁пр = 10А. Таким образом:

i1(t) = 10+ .                                                   (4)

Чтобы определить ток переходного процесса i1(t), необходимо составить систему из двух уравнений, связывающих постоянные интегрирования A1 и A2. Из качественного анализа, в соответствии с 2.1.2, нам известно значение тока i1 непосредственно после коммутации i1(0₊) = 0. Используя выражение (4), получим первое уравнение системы

i1(0₊) = 10 +,

А₁ + А₂ = -10.                                                        (5)