Привод червячной машины для переработки полихлорида. Привод винтового питателя. Определение геометрических параметров передачи

Рассмотрим схему нагружения промежуточного вала, и определим опасные сечения (Рис. 11)

- радиальная сила на колесе, Н; - радиальная сила на шестерне, Н; - окружная сила на колесе, Н; - окружная сила на шестерне, Н; - осевая сила на колесе,H; -осевая сила на шестерне, Н; - реакции опор в вертикальной плоскости, Н; - реакции опор в горизонтальной плоскости, Н; - плечи между точкой приложения силы и опоры соответственно,  - делительный диаметр колеса, мм;  - делительный диаметр шестерни, мм; - плечо действия консольной силы  от муфты до середины опоры, но ввиду того что масса муфты составляет 6,6 кг, этим условием при расчете реакций и параметров вала пренебрегаем.

Исходные данные:

м

 м        

м

м

Н; H

Н;  H

H;   

м;  

Вертикальная плоскость YX:

Определяем опорные реакции (Рис. 11)

Составляем уравнения равновесия моментов и вертикальной плоскости относительно первой и второй опор, и определяем реакции:

             

             

             

        Проверка:

               

Горизонтальная плоскость ZX:

 

Определяем опорные реакции (Рис. 11)

Составляем уравнения равновесия моментов в горизонтальной плоскости относительно первой и второй опор и определяем реакции:

             

             

             

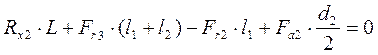
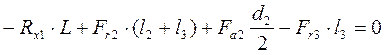
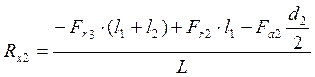
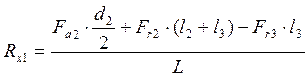
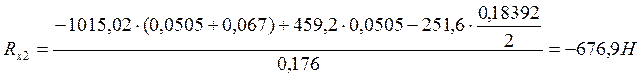
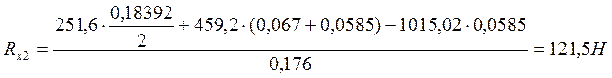
Проверка:

                                

Определяем суммарные реакции:

более нагружена опора№2

Определяем эквивалентную нагрузку:

    где=1-коэффициент радиальной нагрузки;

=0-коэффициент осевой нагрузки;

       т.к                                        

     

Определяем долговечность подшипников на промежуточном валу редуктора в часах:

,

Долговечность подшипников на промежуточном валу редуктора обеспечена.

8.3 Определение реакций опор на тихоходном валу редуктора.

Рассмотрим схему нагружения тихоходного вала, и определим опасные сечения (Рис. 12)

- радиальная сила на колесе, Н; - окружная сила на колесе, Н; - реакции опор в вертикальной плоскости, Н; - реакции опор в горизонтальной плоскости, Н; - плечи между точкой приложения силы и опоры соответственно.

Исходные данные:

м

м

м

Н

Н

 

Вертикальная плоскость YX:

Определяем опорные реакции (Рис. 12)

Составляем уравнения равновесия моментов и вертикальной плоскости относительно первой и второй опор, и определяем реакции.

             

             

             

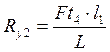
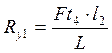
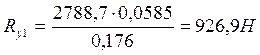
Проверка:

                             

Горизонтальная плоскость ZX:

 

Определяем опорные реакции (Рис. 12)

Составляем уравнения равновесия моментов в горизонтальной плоскости относительно первой и второй опор и определяем реакции:

             

             

             

                

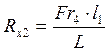
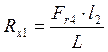
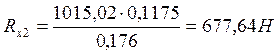
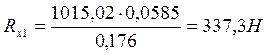
Проверка:

                    

Определяем суммарные реакции:

более нагружена опора№2

Определяем эквивалентную нагрузку:

,

где=1-коэффициент радиальной нагрузки;

=0-коэффициент осевой нагрузки;

       т.к                                                             

Определяем долговечность подшипников на тихоходном валу редуктора в часах:

,

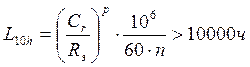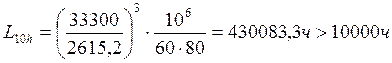
Долговечность подшипников на тихоходном валу редуктора обеспечена.

8.4 Построение эпюр изгибающего момента

Вертикальная плоскость:

Сечение 1-1:

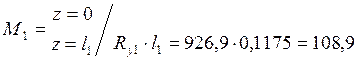
Сечение 2-2: 

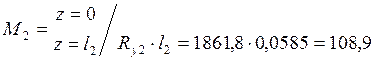
Горизонтальная плоскость:

Сечение 1-1:

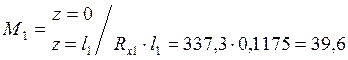
Сечение 2-2: 

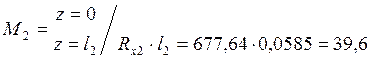
Крутящий момент:

8.5 Определяем опасное сечение под колесом через эквивалентный момент используя третью теорию прочности,  ,

,                                                                                 (88)

где - изгибающий момент в горизонтальной плоскости , Нм;

-изгибающий момент в вертикальной плоскости, Нм;

-вращающий момент тихоходном валу редуктора, Нм;

 

8.6 Проверяем диаметр тихоходного вала в опасном сечении ,мм,

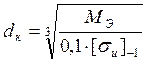,                                                                                          (89)

где - допускаемое напряжение на изгиб при симметричном цикле,

8.7 Определяем величину допускаемого напряжения вычисляем по известной для выбранной стали величине временного сопротивления.

,                                                                                               (90)

где  предел прочности  выбранной стали 45, 660 ;

k – коэффициент запаса прочности принимаем 10.

С учетом переменных напряжений и других факторов .

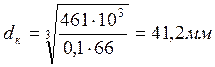
При предварительном расчете валов диаметр вала под колесом конструктивно приняли , т.е. условие прочности вала в опасном сечении выполняется.

Построение эпюр изгибающих моментов:

 

Рисунок 9 – Эпюры изгибающих и крутящих моментов моментов

ведущего вала

Расчет сечения на статистическую прочность:

Результирующий момент:

 

Момент сопротивления кручения:

 

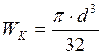
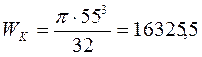
Эквивалентное напряжение:

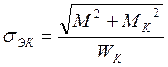
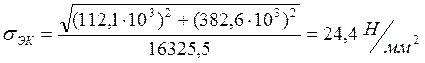
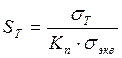
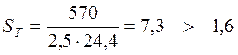
Расчет сечения на сопротивление усталости:

1.  Амплитуда напряжений:

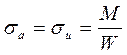
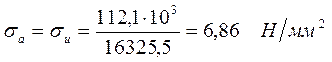
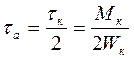
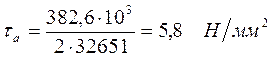
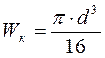
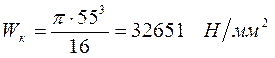
2.  Эффективный коэффициент концентрации напряжений:

                           

3.  Предел выносливости при симметричном цикле изгиба:

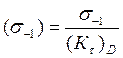
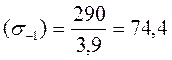 МПа

Предел выносливости при симметричном цикле касательных напряжений:

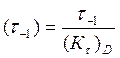
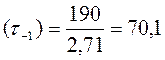 МПа

4.  Коэффициент запаса прочности по нормальным и касательным напряжениям:

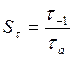
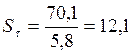
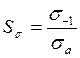
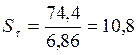
5.  Результирующий коэффициент запаса:

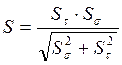
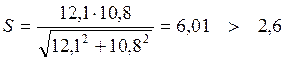
Прочность обеспечена.

Определение реакций опор на ведущем валу редуктора:

Рассмотрим схему нагружения ведущего вала, и определим опасные сечения (Рис. 11)

- радиальная сила, Н; - окружная сила, Н; -осевая сила, Н; - реакции опор в вертикальной плоскости, Н; - реакции опор в горизонтальной плоскости, Н;  - делительный диаметр колеса, мм; - расстояние от точки приложения сил до середины опоры, - расстояние до середины ступицы звездочки от точки приложения сил на колесе;  - сила действующая на валы в ременной передаче, Н.

мм

м

м

Н

Н

Н

Вертикальная плоскость YX:

Определяем опорные реакции (Рис. 10)

Составляем уравнения равновесия моментов и вертикальной плоскости относительно первой и второй опор, и определяем реакции (силу возникающую от веса муфты не учитываем)

             

              

             

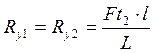
где - окружная сила на шестерне

мм – плечо от точки приложения силы до середины ширины наружного кольца подшипника.

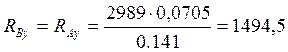
Проверка:

Сечение 1-1:

 

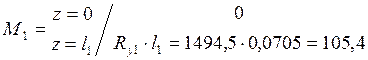
Сечение 2-2: 

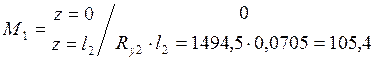
Горизонтальная плоскость ZX:

Определяем опорные реакции (Рис. 8)

Составляем уравнения равновесия моментов в горизонтальной плоскости относительно первой и второй опор и определяем реакции

             

              

             

 

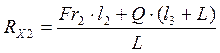
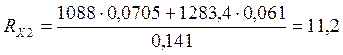
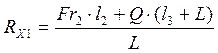
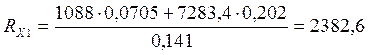
Рисунок 10 – Эпюры изгибающих и крутящих моментов моментов ведомого вала

Проверка:

 

Сечение 1-1:

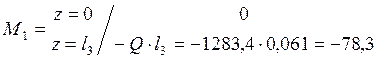
Сечение 2-2: 

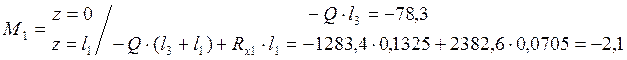
Сечение 3-3:

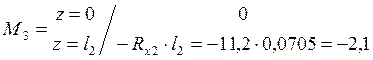
Крутящий момент:

Расчет сечения на статистическую прочность:

Результирующий момент:

Момент сопротивления кручения:

 

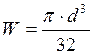
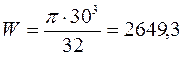
Эквивалентное напряжение:

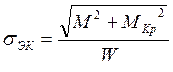
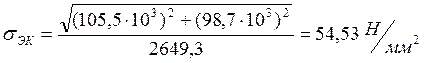
Коэффициент запаса прочности:

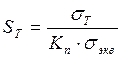
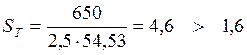
Расчет сечения на сопротивление усталости:

6.  Амплитуда напряжений:

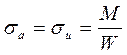
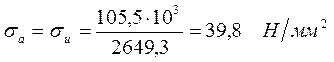
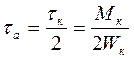
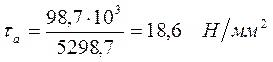
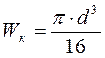
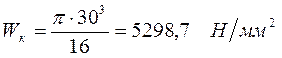
7.  Эффективный коэффициент концентрации напряжений:

                           

8.  Предел выносливости при симметричном цикле изгиба:

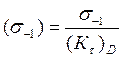
 МПа

Предел выносливости при симметричном цикле касательных напряжений:

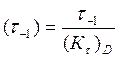
 МПа

9.  Коэффициент запаса прочности по нормальным и касательным напряжениям:

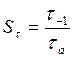
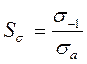
10. Результирующий коэффициент запаса:

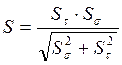
Смазка зубчатых колес редуктора

Смазка зубчатого зацепления осуществляется окунанием, зубчатого венца колеса в масло, заливаемое в картер корпуса.

При  рекомендуется индустриальное масло И 46 А ГОСТ 17794-87.

Зубчатые колеса погружаются минимум на высоту зуба.

Определение объема масла, требуемый для проектируемого редуктора , л

где  кВт – расчетная мощность на ведущем валу редуктора.

 л для проектируемого редуктора требуется 3 литра масла