Расчет стержневой конструкции на сложное сопротивление. Определение размеров поперечных сечений и вычисление напряжений

Федеральное агентство по образованию

Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Курсовая Работа

По дисциплине:  __________________________________________________________

________________________________________________________________________

^{(наименование учебной дисциплины согласно учебному плану)}

Тема: Расчет стержневой конструкции на сложное сопротивление

Автор: ст.гр. ГМ03-2             ____________________                       / Ю. /

^{(подпись)                                               (Ф.И.О.)}

ОЦЕНКА:      _____________

Дата: ___________________

ПРОВЕРИЛ:

Руководитель  проекта              профессор                                      / А.А. /

                                      ^{(должность)                                                                             (Ф.И.О.)}

Санкт - Петербург

2005

Федеральное агентство по образованию

Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

УТВЕРЖДАЮ          

Заведующий кафедрой

_______________________

"____"____________2005 г.

Кафедра механики

КУРСОВАЯ РАБОТА

По дисциплине:Сопротивление материалов

ЗАДАНИЕ

Студенту группы:                ГМ03-2                     ________                   Ю.                                                       

(шифр группы)                 (подпись)                   (Ф.И.О.)

1.  Тема работы: Расчет стержневой конструкции на сложное сопротивление

2. Исходные данные к работе: Выданный вариант

3. Содержание пояснительной записки: Пояснительная записка включает в себя задание на выполнение работы, расчетные формулы, результаты расчета, заключение, библиографический список.

4. Срок сдачи законченного проекта:         

Руководитель проекта:      профессор             ________                 А.А.

(должность)                       (подпись)                                   (Ф.И.О.)

Дата выдачи задания:

АННОТАЦИЯ_ 4

THE SUMMERY_ 4

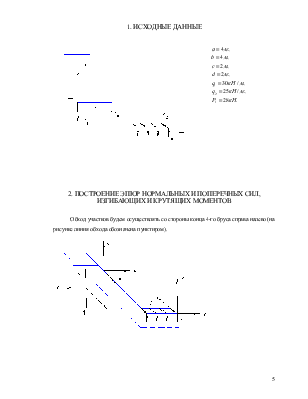
1. ИСХОДНЫЕ ДАННЫЕ_ 5

2. ПОСТРОЕНИЕ ЭПЮР НОРМАЛЬНЫХ И ПОПЕРЕЧНЫХ СИЛ, ИЗГИБАЮЩИХ И КРУТЯЩИХ МОМЕНТОВ_ 5

3. ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ПОПЕРЕЧНЫХ СЕЧЕНИЙ И ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ_ 8

4.ВЫБОР НАИБОЛЕЕ ЭКОНОМИЧНОГО ПРОФИЛЯ_ 15

5.СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ_ 17

АННОТАЦИЯ

Пояснительная записка представляет собой отчет о выполнении курсовой работы. Дано подробное решение стержневой конструкции на сложное сопротивление. Приведена исходная схема конструкции,  построены эпюры поперечных и нормальных сил, а также изгибающих и крутящих моментов.  В конце работы приведен расчет  выбора наиболее экономичного профиля стержня. Дан список используемой литературы.

Страниц 18, 11 рисунков.

THE SUMMERY

The explanatory slip represents the report on performance of course work. The detailed description of process of a presence of dependence of dynamic loading of separate elements of system of a drive from inertia of the engine is given. The theoretical material on those numerical methods of calculation is briefly stated which are necessary for using for the decision of a task. All accounts are made in the programs. At the end of work the final results of calculations are given. The bibliographic links are given.

Pages 18, 11 figures.

1. ИСХОДНЫЕ ДАННЫЕ

2. ПОСТРОЕНИЕ ЭПЮР НОРМАЛЬНЫХ И ПОПЕРЕЧНЫХ СИЛ, ИЗГИБАЮЩИХ И КРУТЯЩИХ МОМЕНТОВ

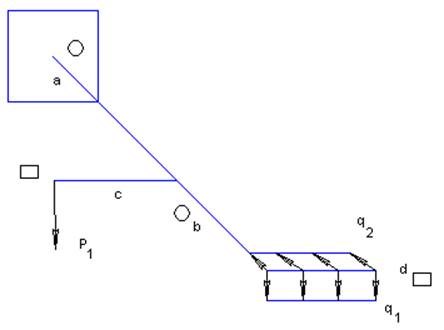
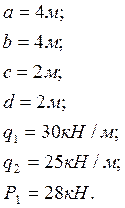
Обход участков будем осуществлять со стороны конца 4-го бруса справа налево (на рисунке линия обхода обозначена пунктиром).

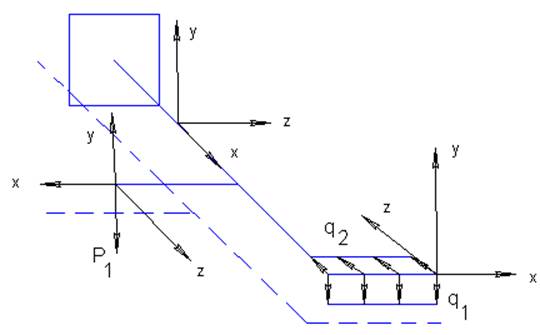
Участок d:

Пользуясь методом сечений, составляют уравнения для внутренних усилий в элементах бруса.

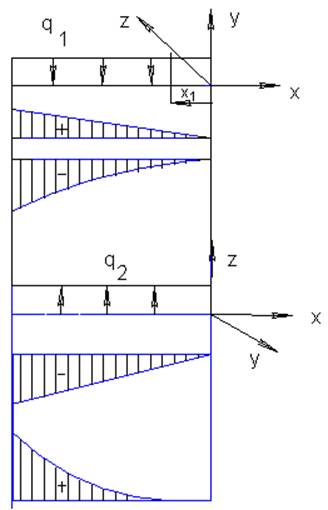На расстоянии х₁ от свободного конца бруса проводиться сечение. В этом сечении (справа) будут действовать:

- от внешней распределенной нагрузки q₁ в плоскости ХОУ  возникает внутреннее усилие Q_y, линейно зависящее от координаты х:

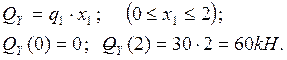
- изгибающий момент от внешней распределенной нагрузки q₁ относительно оси Z будет изменяться по длине бруса по квадратичному закону:

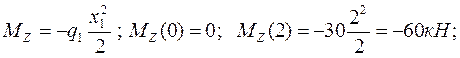
- от внешней распределенной нагрузки q₂ в плоскости ХОZ  возникает внутреннее усилие Q_Z, линейно зависящее от координаты х:

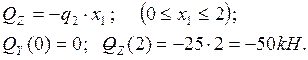
- изгибающий момент от внешней распределенной нагрузки q₂ относительно оси Y будет изменяться по длине бруса по квадратичному закону:

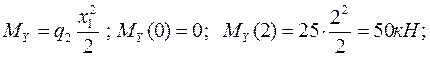
-Нормальная сила:

-Крутящий момент: 

При написании уравнений и построение эпюр должно быть учтено правило знаков при изгибе балок.  Условлено считать поперечную силу Q положительной, если внешние силы, лежащие слева от проведенного сечения, направлены вверх, или справа от него – вниз. Изгибающий момент считается положительным, если алгебраическая сумма моментов сил, расположенных слева от сечения, дает равнодействующий момент, направленный по ходу часовой стрелки; либо для правой части балки, если равнодействующий момент сил, лежащих правее сечения, направлен против хода часовой стрелки.

Участок с:

Сечение бруса проводиться на расстояние х₂ от  свободного конца.

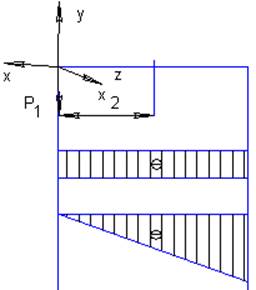От внешней нагрузки P₁ в плоскости ХОУ возникает внутреннее усилие Q_y, распределенное по длине балки по линейному закону:

Возникающий от силы Q_Y изгибающий момент М_z зависит от координаты х в первой степени:

Нормальная сила:

Крутящий момент: 

Участок b:

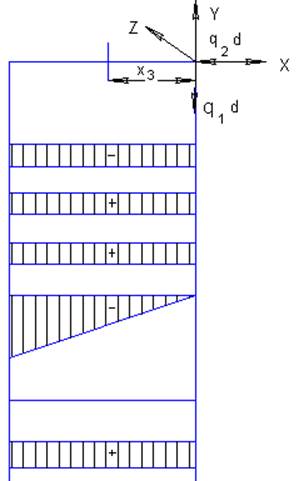На расстоянии х₃ от свободного конца бруса проводиться сечение.

Внешняя распределенная нагрузка q₁ приводиться к внутреннему усилию Q_Y:

Эта же сила вызывает изгибающий момент М_Z.

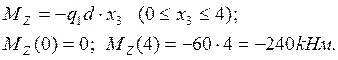
Поперечная сила в плоскости XOZ:               

Изгибающий момент относительно оси У: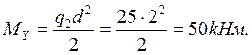 

Нормальная сила:

Крутящий момент: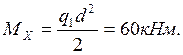

Участок a:

Возьмем четвертое сечение х₄ от свободного конца этого бруса.

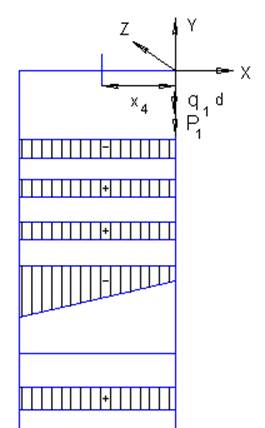Внешняя распределенная нагрузка q₂ является сжимающей силой