Сущность способа и область его применения. Схема холодильной станции. Схема циркуляции хладоагента. Коэффициент температуропроводности породы

Если количество рядов замораживающих колонок будет больше, чем 2, то расчет времени замораживания для смыкания ледопородных цилиндров крайних рядов производят по формуле (28), а для внутренних рядов по формуле

                                                (29)

При проходке шахтных стволов с использованием замораживания пород колонки располагают по окружности так, чтобы после образования ледопородной стенки в виде полого цилиндра внутренний его диаметр был равен диаметру ствола в проходке. В процессе формирования ледопородной стенки при сооружении шахтных стволов теплоприток к внешней стороне ледопородного полого цилиндра со временем будет уменьшаться до некоторого значения. Теплоприток к внутренней стороне ледопородного полого цилиндра будет уменьшаться значительно быстрее, чем с внешней стороны, пока не прекратится совсем.

Выражение для определения времени образования ледопородного ограждения вокруг шахтного ствола имеет следующий вид:

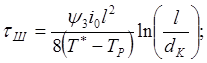                                                        (30)

где

                                                                       (31)

ТЕМПЕРАТУРНОЕ ПОЛЕ В ЛЕДОПОРОДНЫХ ОГРАЖДЕНИЯХ

Температурное поле при формировании одиночного ледопородного цилиндра описывается выражениями (11) и (12).

В процессе формирования ледопородных ограждений температурное поле изменяется во времени и в пространстве. До того момента, пока отдельные ледопородные цилиндры не сомкнулись, их изотермы при температуре от T_P до T^* в плане будут представлять концентрические окружности. При смыкании смежных ледопородных цилиндров их нулевые изотермы соединятся. По мере увеличения толщины ледопородного ограждения в замке, изотермы вокруг замораживающих колонок будут представлять собой параллельные между собой волнообразные кривые, гребни которых располагаются напротив осей колонок.

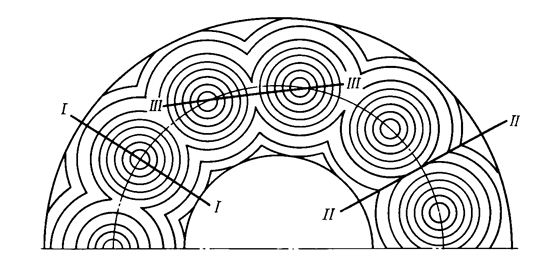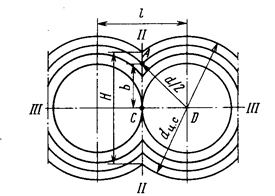
Рис. 12. Характер распределения изотерм в ледопородном ограждении.

1. Главная плоскость I - I проходит через оси замораживающих колонок перпендикулярно к линии их расположения.

2. Замковая плоскость II - II проходит через замковую линию, параллельно осям замораживающих колонок и перпендикулярно к линии их расположения.

3. Осевая плоскость III - III проходит через оси двух смежных замораживающих колонок.

В каждой из этих плоскостей распределение температур имеет свои особенности и описывается различными уравнениями. В главной плоскости распределение температур аналогично одиночному ледопородному цилиндру и описывается следующим уравнением:

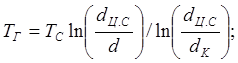                                                   (32)

где T_C - температура наружной стенки замораживающей трубы, °С;

d_Ц.С - диаметр ледопородного цилиндра, соответствующий ледопородному ограждению с толщиной H в замке, м;

d - текущее значение диаметра ледопородного цилиндра в главной плоскости, м.

В той половине главной плоскости, которая находится во внутренней части ледопородного ограждения, градиент температуры по радиусу несколько выше, чем в наружной ее части.

Так как процесс образования ледопородного ограждения очень длителен по времени, то, как это следует из уравнения (32), распределение температурного поля не зависит от свойств замораживаемой породы.

Уравнение (32) позволяет оценить расстояние от центра замораживающей колонки, где располагается заданная изотерма. Для этого необходимо его решить относительно d,

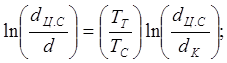                                                   (33)

Так как

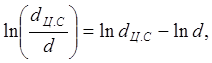
то

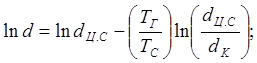                                             (34)

Обозначив правую часть уравнения (34) через B и пропотенцировав ее, получим выражение для определения радиуса расположения изолинии с заданной температурой в главной плоскости

                                                           (35)

Так как любые точки замковой плоскости находятся на одинаковом расстоянии от осей смежных замораживающих колонок, то они должны удовлетворять уравнению (35).

Обозначим через d текущее значение диаметра ледопородного цилиндра при увеличении его от d_Ц до d_Ц.С (рис. 13), имеем

                                                                      (36)

Подставляя значение  d из выражения (36) в (32), получим уравнение для определения температуры ледопородной стенки в замковой плоскости T_З, в зависимости от расстояния b до осевой плоскости:

                           (37)

При b = 0 уравнение (37) примет вид

                                          (38)

а при b = H/2

                            (39)

Так как , то согласно (39) T_З = 273 К, т. е. на границе ледопородного ограждения температура равна температуре замерзания воды.

Из уравнения (37) можно определить расстояние b от осевой плоскости