Исследование корреляции многих переменных. Получение уравнения множественной регрессии и коэффициента множественной корреляции для четырёх параметров

Федеральное агентство по образованию

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

 

Кафедра обогащения полезных ископаемых

Расчетно-графическое задание №2

По дисциплине: Основы научных исследований

ИССЛЕДОВАНИЕ КОРРЕЛЯЦИИ МНОГИХ ПЕРЕМЕННЫХ

Выполнила студентка гр.ОП-02:

Проверила: ассистентка

 

Санкт-Петербург

2006

ИССЛЕДОВАНИЕ КОРРЕЛЯЦИИ МНОГИХ ПЕРЕМЕННЫХ

Цель работы: получение уравнения множественной регрессии и коэффициента множественной корреляции для четырёх параметров.

Общие сведения

Для четырёх переменных  линейное уравнение множественной регрессии:

x_1,2,3,4 – среднее значение функции х₁, соответствующее заданным значениям аргументов x₂,x₃,x₄.

Для упрощения расчётов сделаем замену переменных и выразим все зависимости в стандартизованном масштабе:

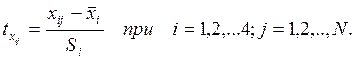
В новом (стандартизованном) масштабе уравнение регрессии

, где – среднее значение стандартизованной переменной t₁, соответствующее заданным значениям t₂,t₃,t₄;  – стандартизованные коэффициенты множественной регрессии; – стандартизованные значения переменных.

Стандартизованные коэффициенты находят методом наименьших квадратов:

что приводит к системе линейных уравнений:

Решая эту систему, находим коэффициенты

Уравнение множественной регрессии в натуральном масштабе получается пересчетом коэффициентов:

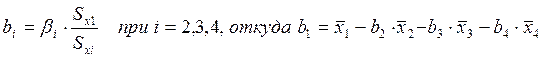
коэффициент множественной регрессии:

.

выполнения работы

Исходные данные согласно варианту №7 представлены в таблицах 1 и 2.

Таблица 1

Матрица парных коэффициентов корреляции

Переменные	Y	X1	X2	X3
X1	-0,606	1,000	0,460	-0,254
X2	-0,450	0,460	1,000	-0,280
X3	0,458	-0,254	-0,280	1,000

Таблица 2

Числовые характеристики переменных

Числовые характеристики	Наименование переменных
	Вода в зумпф, м3/ч - X1	Производительн.мельницы,т/ч-X2	Вода в мельницу м3/ч - X3	Мощность мель- ницы,% шкалы-Y
Среднее арифметическое	413,10	326,16	34,36	49,20
Среднее квадратическое	53,60	28,30	1,07	4,18

у – мощность насоса, %;

х₂ – вода в зумпф;

х₃ – плотность слива;

х₄ – вода в мельницу.

       ;         

      ;        

Составляем систему линейных уравнений:

-0,606  =  1,00   + 0,460 + (-0,254)

-0,450  = 0,460  + 1,00  + (-0,280)

0,458  = (-0,254)  + (-0,280) + 1,00

Решая эту систему методом Крамера, находим коэффициенты   

Уравнение множественной регрессии в натуральном масштабе получается пересчетом коэффициентов:

;

;

;

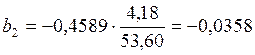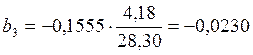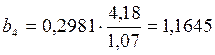Коэффициент множественной корреляции:

.

Для четырёх переменных  линейное уравнение множественной регрессии:

.

Вывод: из уравнения множественной регрессии видно, что не все дополнительные аргументы действуют на функцию положительно, наибольшее влияние оказывает вода, подаваемая в мельницу (т.к. наибольшее абсолютное значение стоит перед х₄). Степень влияния коэффициентов корреляции можно интерпретировать следующим образом: наиболее сильное влияние на функцию оказывает вода, подаваемая в мельницу; следующая по степени влияния – вода, подаваемая в зумпф; наименьшее влияние – плотность слива. Причем, вода в мельницу влияет прямопропорционально, т.к. ее значение положительно, а вода в зумпф и плотность слива – обратнопропорционально, т.к. их значения отрицательны. Коэффициент множественной корреляции больше максимального значения коэффициентов корреляции. Проанализировав все данные, можно сказать, что добавление аргументов не лучшим образом влияет на качество модели.