Комплексная задача по кинематике точки. Определение траектории точки. Модули скорости и ускорения. Определение положения точки и ее кинематических характеристик в данный момент времени

Министерство образования Российской Федерации

Санкт-Петербургский  государственный горный  институт им. Г.В. Плеханова

(технический университет)

Кафедра механики

Расчетно-графическое задание №2

Комплексная задача по кинематике точки.

Вариант 3

Выполнил: студент группы ГГ-02       _______________     / /

                                                ^{( должность)                                             (подпись)                                       (Ф.И.О.)}  

ОЦЕНКА: _____________

Дата: __________________

ПРОВЕРИЛ:

Руководитель:  профессор                  ________________         / /

                                           ^{(должность)                                                   (подпись)                                             (Ф.И.О.)}

Санкт-Петербург

2003 год

Задание:

Движение точки задано координатным способом. Необходимо найти траекторию точки и вычертить ее; скорость, ускорение и касательное ускорение точки в функции времени; скорость, ускорение, касательное ускорение, нормальное ускорение и радиус кривизны траектории в момент времени t₁. Векторы показать на рисунке.

Дано:              .

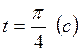Решение:

A) Определение траектории точки.

Исключим время t из уравнений движения:

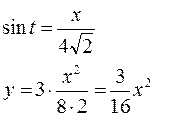
Мы получили параболу, симметричную относительно оси ординат.Из условий   

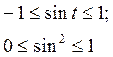следует, что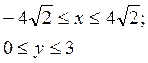

Это значит, что траекторией является не вся парабола, а только её часть, изображенная на рис. сплошной линией.

В) Определение скорости и ускорения точки, а так же её касательного ускорения в зависимости от времени. Запишем формулы:

Модули скорости и ускорения:

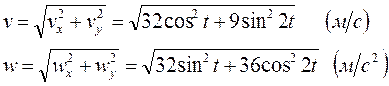
При 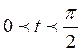 координата х возрастает, а у убывает,т.е. точка из начального положения  движется по правой ветви вверх. Направим ось  как показано на рис.Тогда на взятом интервале времени ,и касательное ускорение точки

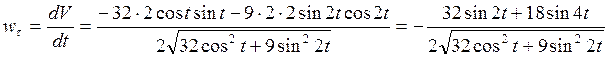
C) Определение положения точки и ее кинематических характеристик в данный момент времени. При 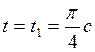 имеем:

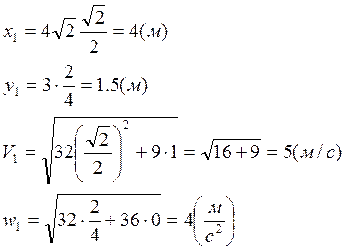
Заметим, что   ,  поэтому вектор  горизонтально влево:

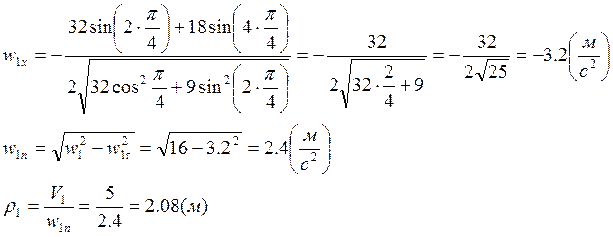
Где - радиус кривизны момент t₁.