Изучение влияния характеристик жесткости связей колесной пары с конструкцией тележки. Изучение вынужденных колебаний 8-осного вагона с вязким трением в подвешивании, страница 3

10. Имя первого рабочего файла в Matlabe - ust4kp.m

11. Имя второго рабочего файла в Matlabe - ust4kp1.m

                    Понятия. Определения. Критерии

Работы Ляпунова позволили, в частности, установить следующее.

Устойчивость данного невозмущенного движения означает, что при достаточно малых начальных возмущениях возмущенное движение сколь угодно мало отличается от невозмущенного движения. Если же невозмущенное движение неустойчиво, то возмущенное движение будет отходить от него, как бы малы ни были начальные возмущения.

Невозмущенное движение называется асимптотически устойчивым, если любое возмущенное движение стремиться к невозмущенному.

В большинстве задач динамики дифференциальные уравнения малых колебаний относительно положения равновесия (поступательного установившегося движения) являются уравнениями возмущенного движения системы. При этом обобщенные координаты рассматриваются как малые возмущения, а их значения при невозмущенном движении принимаются равными нулю.

По уравнениям движения динамической системы известными методами можно получить характеристическое уравнение, определяющее собственные числа матрицы M, составленной из коэффициентов при неизвестных в уравнениях движения системы записанных в нормальной форме. Степень характеристического уравнения равна порядку nсистемы дифференциальных уравнений описывающих движение.

В общем случае характеристическое уравнение представляется выражением:

                               a₀ⁿ+a₁^n-1+...a_n-1+a_n = 0,                   (1)          

где  - переменная, принимающая значения собственных чисел матрицы M при выполнении условия (1);

       n -  порядок системы дифференциальных уравнений.

Уравнение (1) имеет, в общем случае, n/2 сопряженных комплексных корней. По корням этого уравнения ( или, что то же, по собственным числам матрицы M ) можно судить о свойстве устойчивости динамической системы ( например,  вагона или колесной пары ) следующим образом.

1.  Если вещественные части всех корней характеристического уравнения отрицательны, то невозмущенное движение асимптотически  устойчиво.

2.  Если среди корней характеристического уравнения имеется хотя бы один, вещественная часть которого положительна, то невозмущенное движение неустойчиво.

3.  Если вещественные части некоторых корней равны нулю, а вещественные части остальных отрицательны, то невозмущенное движение устойчиво но не асимптотически.

Уравнения движения

Для выбора расчетной схемы примем следующие допущения:

1) по динамическим характеристикам колесная пара и путь симметричны относительно продольной вертикальной плоскости;

2) между колесной парой и рамой тележки установлены упругие связи;

3) силы в контакте колесо- рельс (силы крипа) пропорциональны относительной скорости проскальзывания контактных поверхностей.

Уравнения движения колесной пары, как уравнения равновесия действующих сил и моментов, составленные на основе использования принципа Д’аламбера, имеют вид

 F_cy1 - F_cy2  + Y₁ + Y₂ ;

= F_cy1b - F_cy2b + X₁s+ X₂s,                        (1)

где y, - обобщенные координаты;

          F_cy1, F_cy2 - реакции связей на их деформацию вдоль оси Y;                  

          F_cx1, F_cx2 - то же, вдоль оси X ;

          X₁, X₂, Y₁,Y₂ -составляющие сил крипа в пятнах контакта 1 и 2;

          2b - расстояние между серединами шеек;

          2s - расстояние между кругами катания.

Реакции упругих связей представляются выражениями:

F_cx1= - c_xb;          F_cy1= - c_y b;

F_cx2=  c_xb;           F_cy2=  c_y b,                  (2)

где  c_x, c_y - коэффициенты жесткости связей при их деформации вдоль осей X и Y, соответственно.

Силы крипа (псевдоскольжения), действующие в пятнах контакта колеса и рельса, согласно теории Картера можно представить в виде

X₁ = - F_x (s+y₁);

                                X₂ = - F_x (-s-y₂);                            (3)

Y₁ = Y₂= - F_y (-s),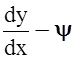

где   F_x ,F_y -коэффициенты Крипа при проскальзывании контактных поверхностей колеса и рельса вдоль осей  X и Y, соответственно;

n, r - радиус колеса и уклон поверхности катания.

Использовав выражения, определяющие реакции связей (2) и силы крипа (3) и перейдя от производных по времени к производным по координате x в уравнениях (1) получим уравнения движения в форме (4), в которой коэффициенты при неизвестных зависят и от скорости движения

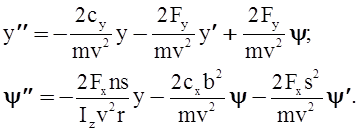           (4)

При переходе к производным по координате xиспользованы следующие соотношения, полученные с учетом постоянства скорости движения в достаточно малом интервале времени, например, для обобщенной координаты y

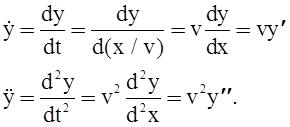
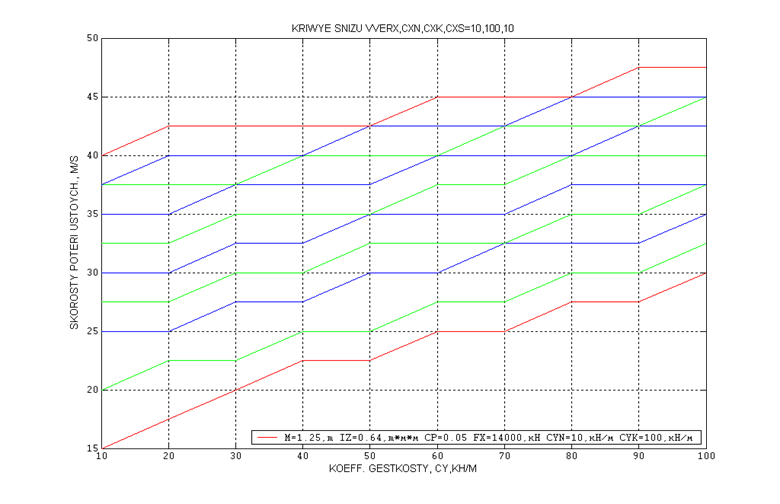
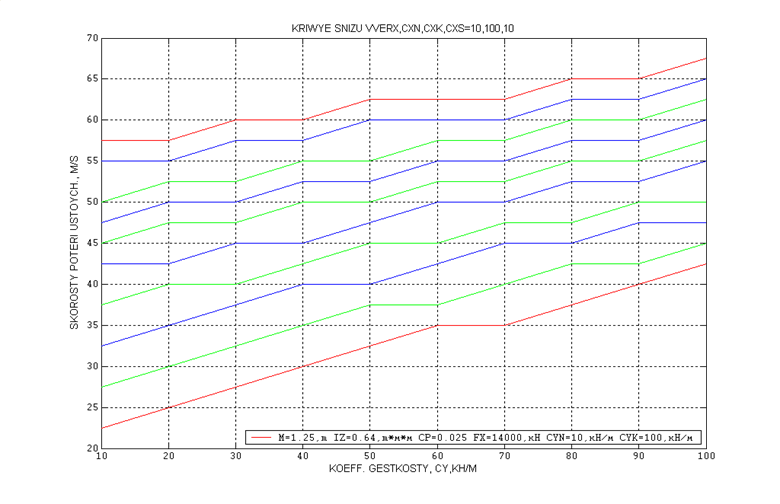
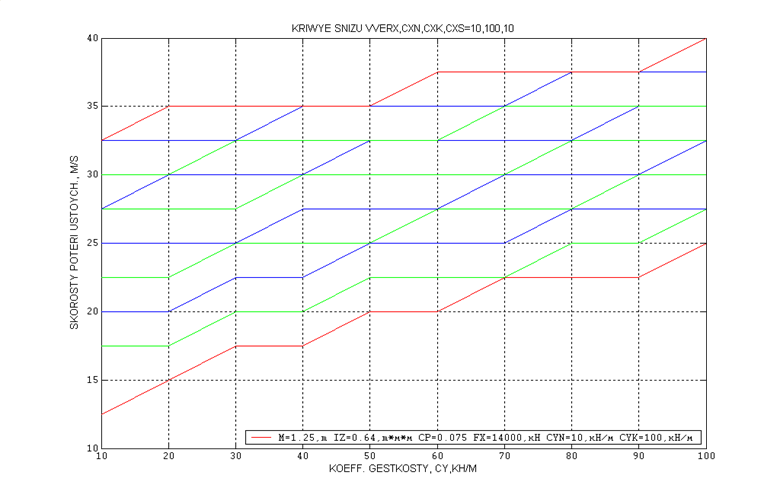
            Выводы:

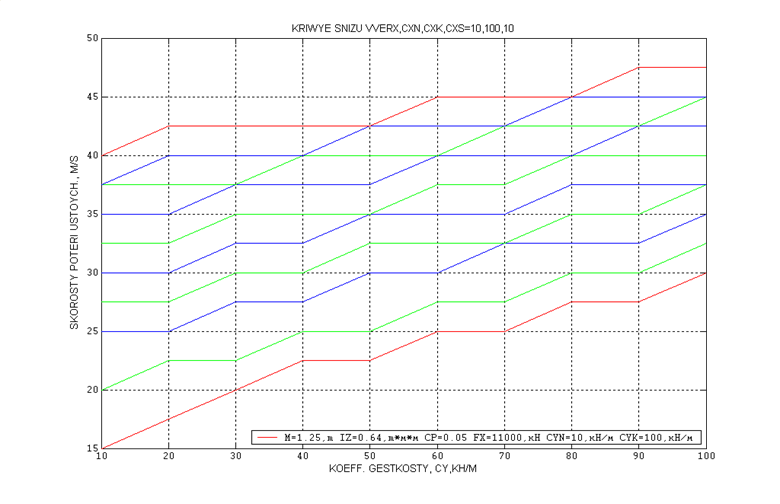
1) При малых   жесткостях   (Сx и Сy от  10 до 100 кН/м) можно подобрать такую  жесткость,  при

   которой движение устойчиво  до    скорости 65 м/с . Это происходит при Сx=100 кН/м, Сy=80-90 кН/м, независимо от силы крипа:

Fx=11000 кН, Fx=14000 кН, Fx=18500 кН.

2) При   больших жесткостях  (Сx и Сy от 100 до 1000 кН/м)    можно подобрать  такую  жесткость,

   для которой   при скорости движения до 210 м/с сохранялась устойчивость .Это происходит

   при Сx=1000 кН/м, Сy=700-800 кН/м, но при условии, что силы крипа не будут превышать Fx=11000 кН.

 Таким образом, изменяя продольную и поперечную жесткость можно повысить скорость устойчивого движения. Оптимальной является продольная жесткость, лежащая в интервале Сx=10 – 100 кН/м. Поперечная же жесткость уменьшается в зависимости от величины продольной и лежит в большом интервале Сy=10 – 100 кН/м. Так, например, при различных сочетаниях продольной и поперечной жесткости движение устойчиво до скорости 65 м/с.