Плотность вероятности системы. Двойной интеграл от плотности по прямоугольник. Плотность нормированная функция

распределения системы F(x,y) непрерывна на всей плоскости xOy и имеет внутри области  непрерывную смешанную производную второго порядка.

Определение 2.  Плотностью вероятности системы (X,Y) в точке (x,y) называется предел отношения вероятности попасть в некоторую область D, содержащую эту точку, к площади D при условии, что область D стягивается в эту точку.

Плотность вероятности системы или просто плотность обозначается f(x,y) и называется также дифференциальной функцией распределения или дифференциальным законом распределения  системы.

Возьмем произвольную точку (x,y)  и рассмотрим прямоугольник с вершиной в этой точке и сторонами и . На основании определения 2 можно написать

f(x,y) = lim.

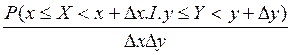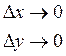
Используя формулу (2.2) и правило последовательного перехода к пределу , получим

f(x,y) = lim           =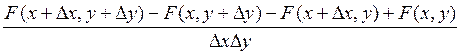

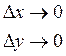
= lim           - =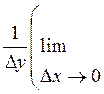

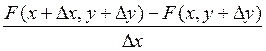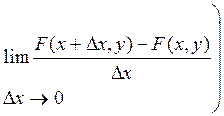= lim=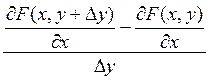

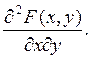
y

 Рассмотрим двойной интеграл от плотности по прямоугольнику представленному на рисунке 1.

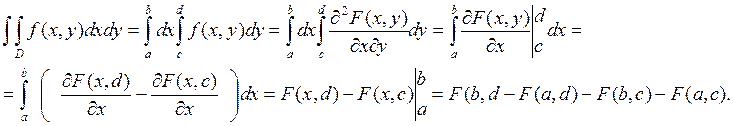
В соответствии с формулой (2.2) получаем

P (a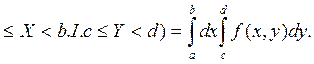       (3.1)

Эта формула легко обобщается на всю плоскость xOy , считая , что за пределами области  (области допустимых значений системы) она равна 0.

Тогда, используя формулу (3.1), можно легко получить все свойства плотности.

1.  Плотность неотрицательна на всей координатной плоскости. Действительно, она является пределом неотрицательной величины по определению, поэтому f(x,y)0.

2.  Плотность нормированная функция, т.е.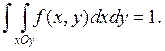

Действительно, на основании формулы (3.1) и свойств функции распределения получим

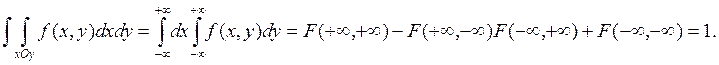
3.  По плотности системы можно найти ее функцию распределения по формуле

                            F(x,y) =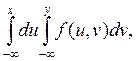                   (3.3)

(отметим , что для того , чтобы различать переменные интегрирования и пределы интегрирования , мы воспользовались независимостью интеграла от названий переменных интегрирования).

Действительно,

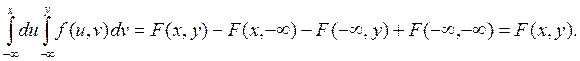
4.  Плотность случайной величины X  системы (X,Y) определяется по формуле

f₁(x) = 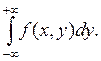                                                  (3.4)

Действительно ,

=

=

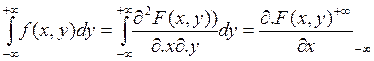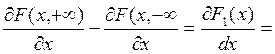
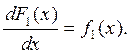
Аналогично определяется и плотность величины Y

f₂(y) = 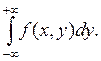                                                  (3.5)

5.  Теперь, зная плотность системы, можно найти математические ожидания и дисперсии случайных величин, составляющих систему

M(X) = 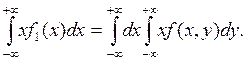                  (3.6)

Аналогично

M(Y) = 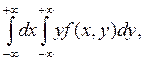                                      (3.7)

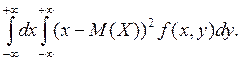D(X) =                     (3.8)

Дисперсию можно находить и по ее свойству

D(Y) = 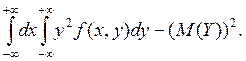                    (3.9)

Пример 2. Система случайных величин (X,Y) распределена равномерно внутри круга

x²+y²=r², т.е. плотность на области , которая представляет круг радиуса r, постоянна f(x,y)=c. Тогда, на основании свойства нормированности плотности и учитывая, что за пределами области  плотность равна 0, получаем

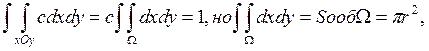
поэтому 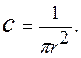Теперь найдем плотность случайной величины X – f₁(x)=,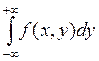

но так как для каждого x  Y изменяется в пределах от -до

, то      f₁(x) = . 

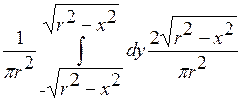Аналогично, в силу симметричности, f₂(y) = 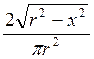. Тогда

М(X) = 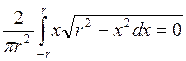  и M(Y)=0.

D(X) = M(X²) = 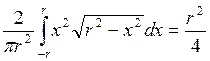 и D(Y) = .

2.  Условные плотности. Регрессия.

Рассмотрим непрерывную случайную величину X . имеющую плотность f₁(x). Возьмем произвольное значение x из области возможных значений этой величины и дадим ему приращение dx, причем столь малое, что событие хX<x+dx можно считать равным событию X=x, т.е.

                                (хX<x+dx) = (X=x),                                 (4.1)

тогда событию Х=х можно присвоить вероятность

P(X=x)=P(xX<x+dx)=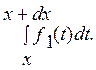

Применив к этому интегралу теорему о среднем , получим

P(X=x)=

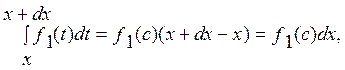
причем с и, следовательно, в соответствии с (4.1) можно считать , что

с=х, т.е.

                                               P(X=x)=f₁(x)dx.                           (4.2)

Аналогично этому  для системы непрерывных случайных величин (X,Y) , имеющих плотность f(x,y), можно считать , что

P(X=x&Y=y)=P(xX<x+dx&yY<y+dy)=f(x,y)dxdy     . (4.3)

    Плотность случайной величины (Y/X=x) называется условной плотностью случайной величины Y при условии, что X=x  и обозначается f₂(y/х). Эта функция двух переменных, а косая черта является признаком условной плотности по аналогии с условной вероятностью P(A^,/В). Тогда в соответствии с формулой (4.1) можно написать

P(Y=y/X=x)=f₂(y/x)dy.                                 (4.4)

На основании теоремы умножения имеем

P(X=x &Y=y)=P(X=x) P(Y=y/X=x) ,

и учитывая формулы (4.2)-(4.4), получим

f(x,y)dxdy = f₁(x)dxf₂(y/x)dy ,                       

отсюда условная плотность

f₂(y/x) = 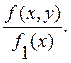                                          (4.5)

Аналогично определяется условная плотность случайной величины Х при условии , что Y=y

F₁(y/x) = 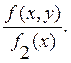                                         (4.6)

Условным плотностям, определяющим условные законы распределения, соответствуют условные математические ожидания и условные дисперсии, которые находятся по формулам :

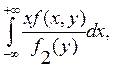М(X/y) = (x/y)dx =                                                      (4.7)

M(Y/x) = (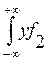y/x)dy =  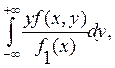                                                (4.8)

D(X/y) = 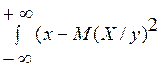f₁(x/y)dx = f₁(x/y)dx-(M(X/y))².

Аналогично определяется и условная дисперсия D(Y/x).

В соответствии с формулой (1.5) каждому значению одной дискретной случайной величины соответствует условное математическое ожидание другой. Это позволяет составить таблицы зависимостей условных математических ожиданий одной величины от значения другой (табл. 4 и табл. 5).