РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 1
Разработать рекурсивный алгоритм, написать реализующую его рекурсивную подпрограмму на С++ и проверить на тестовых данных.
Варианты заданий
1. Имеются гири весом w0, w1, …, wn-1. Надо определить, можно ли из них составить сумму, равную p. В случае положительного ответа вывести веса гирь, составляющих этот вес.
2. С клавиатуры вводится алгебраическое выражение, состоящее из целых чисел, скобок и операций ‘–‘ ( унарный минус ), ‘<’ ( сдвиг влево ), ‘>’ ( сдвиг вправо ). Вычислить значение этого выражения.
3. Определить такую рекурсивную функцию, что ее значение fix( f, a, b, eps ) равно корню уравнения x = f(x) на отрезке [a, b], с точностью eps. Известно, что функция f непрерывна и отображает отрезок [a, b] в себя. Для нахождения приближенного значения корня рекомендуется использовать метод деления отрезка пополам.
4. Вычислить значение логического выражения, заданного с клавиатуры, состоящего из натуральных чисел, скобок и операций ‘&’ (поразрядное логическое ‘и’) и ‘~’ (поразрядное логическое ‘не’). Например, ~8 & (64 & 125) будет равно 11110111 & 1000000 = 64. Операции ‘&’ и ‘~’ предполагаются имеющими одинаковый приоритет.
5. Вычислить наибольший общий делитель двух натуральных чисел, введенных с клавиатуры.
6. Имеются гири весом w0 < w1 < … < wn-1. Для каждого из чисел wi достаточное число гирь веса wi. Какое минимальное число гирь необходимо для получения суммарного веса t ?
7. Символьная строка t называется обращением строки s, если ее длина равна длине строки s, а символы расположены в обратном порядке. Например, обращением строки s = “abcbc” является t = “cbcba”. Написать подпрограмму обращения строки, имеющую прототип
void revers( char *s, int i, int j );
вызывающуюся как reverse( t, 0, strlen(t) ).
8. Определить рекурсивную функцию int Lat, возвращающую количество латинских букв в текстовом файле.
9. Найти все цифры в текстовом файле и вывести их в обратном порядке.
10. Заданы целое число x и текстовый файл, содержащий записанные через пробелы целые числа. Вывести сначала все числа, меньшие Х, а затем все остальные.
11. Вычислить сумму
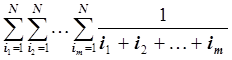
Указание. Обозначить P(N, m, i) = 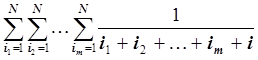 и
доказать соотношение P(N, m, i ) =
и
доказать соотношение P(N, m, i ) = 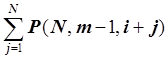 . Тогда искомая
сумма равна P(N, m,
0).
. Тогда искомая
сумма равна P(N, m,
0).
12. С клавиатуры вводится логическое выражение, состоящее из булевых констант 0 (ложь) и 1 (истина), скобок и логических символов Ú (“или”) и Ø (“не”). Написать программу вычисления значения этого логического выражения.
13. Имеются гири весом w0 < w1 < … < wn. Гирь каждого веса – любое достаточное количество. Найти хотя бы один набор гирь, в сумме дающих заданное с клавиатуры число. Например, для гирь 2 < 3 < 5 и числа 6, таким решением будет сумма 3 + 3 (или 2 + 2 + 2).
14. Задан текстовый файл. Вывести сначала содержащиеся в нем цифры, а затем – латинские буквы в обратном порядке.
15. Вычислить коэффициенты a[0], a[1], …, a[n-1] многочлена
p(x) = a[0] + a[1]x + … + a[n-1]xn-1 + xn, если известны его действительные корни x[1], x[2], …, x[n].
Указание. Обозначив через a(n, i) коэффициент a[i] многочлена степени n, легко получить рекуррентные соотношения, с помощью теоремы Безу:
a(n, n-1) = a(n-1, n-2) – x[n]
a(n, i) = a(n-1, i-1) – a(n-1, i) * x[n], 1 £ i < n-1
a(n, 0) = - a(n-1, 0) * x[n]
Значения a(n, i) для всех 0 £ i £ n-1 вычисляются с помощью рекурсивной функции, построенной по этим соотношениям.
16. Задана матрица a[i][j] цен на авиабилеты между городами i и j. Всего рассматривается 6 городов. Генерируя перестановки (i1, i2, i3, i4, i5), найти путь коммивояжера
0, i1, i2, i3, i4, i5, 0
минимальной стоимости и записать его в массив int b[7].
17. Две примыкающие равные строки называются идентичными подтекстами, например, строка “abcdecde” содержит идентичные подтексты “cde”. Используя рекурсивную функцию, проверить слово на присутствие смежных идентичных подтекстов. Под словом понимается строка, состоящая из букв и цифр.
18. Задан текстовый файл. Игнорируя пробелы, вывести сначала все цифры, а затем – остальные символы в обратном порядке.
19. Найти число B(m) всех разбиений множества, состоящего из m элементов (число Белла). Воспользоваться формулой
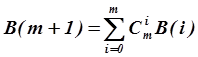
и значением B(0) = 1.
20. Построить треугольную таблицу для чисел разбиений S(m, n) множества {1, 2, …, m} на n блоков (чисел Стирлинга второго рода), при 0 £ n £ m. Воспользоваться соотношениями S(m, 0) = 0, при m > 0; S(m, m) = S(0, 0) = 1; S(m, n) = 0, при n > m; S(m, n) = S(m-1, n-1) + nS(m-1, n), при 1 £ n £ m.
21. Задан текстовый файл, содержащий целые числа, записанные через пробелы. Вывести сначала все четные числа, а затем в обратном порядке все нечетные числа, делящиеся на 3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.