Рекурсивный алгоритм. Определение рекурсивной функцию int Lat, возвращающую количество латинских букв в текстовом файле, страница 2

22.  Имеется набор монет (p₀, p₁, …, p_n-1) по одной монете каждого достоинства. Определить, можно ли этими монетами разменять сумму q.

23.  Написать рекурсивную подпрограмму проверки строки символов на симметричность. Функция должна вызываться как t=sym(s, strlen(s)), где строка определена как char s[], и возвращать значение t=1 если строка симметрична и t=0 в противном случае.

24.  Текстовый файл содержит числа с плавающей точкой, записанные через пробелы. Вывести отрицательные числа в обратном порядке.

25.  Написать рекурсивную подпрограмму для вычисления значений функции       f(int n), заданной с помощью рекуррентного соотношения

Здесь - целая часть дроби, полученной делением n на i.

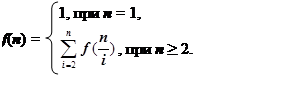26.  Вычислить число двоичных деревьев T(n), имеющих n вершин, с помощью рекуррентного соотношения

T(n+1) = T(0) T(n) + T(1) T(n-1) + … + T(i) T(n-i) + … + T(n)T(0).

Проверить формулу 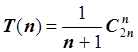 для n ≤ 5, применяя для вычисления  соотношения ,

27.  С клавиатуры вводится логическое выражение, состоящее из целых чисел, логических операций & и | и скобок. Вычислить значение этого логического выражения, если операции & и | вычисляются поразрядно и имеют равные приоритеты.

28.  Текстовый файл состоит из слов, записанных через пробелы. Слова состоят из латинских букв и цифр. Вывести сначала прописные (большие), а потом строчные (маленькие) буквы в обратном порядке. Цифры не выводить.

29.  С клавиатуры вводится арифметическое выражение, состоящее из целых чисел, операций ‘*’ и ‘%’ (остаток от деления) и скобок. Написать программу для вычисления этого выражения.

30.  Число f(n) путей на двумерной целочисленной решетке, не имеющих самопересечений и состоящих из n звеньев типа (1, 0), (-1, 0) и (0, 1), удовлетворяет соотношениям:

f (n) = 2f (n-1) + f (n-2),   f (0) = 1,   f (1) = 3.

Вычислить f(n) и проверить с точностью 0.01 формулу

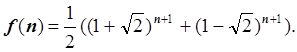
Примеры выполнения задания 1

Пример 1

Имеется положительное число t и конечная последовательность положительных натуральных чисел (весов) w₀, w₁, …, w_n. Необходимо определить, можно ли из этих весов выбрать такой их набор, чтобы сумма чисел из этого набора точно равнялась величине t. Например, если t = 10 и последовательность весов состоит из чисел 5, 4, 4, 1, то можно выбрать первый, второй и четвертый веса, поскольку 10 = 5 + 4 + 1; если     t = 13,  то можно выбрать первый, второй и третий, поскольку 13 = 5 + 4 + 4; если t = 15, то решений нет.

Решение

Построим алгоритм на основе рекуррентного соотношения для функции  knapsack(s, i), принимающей значение 1, если существует набор весов из последовательности w_i+1, w_i+2, …, w_n, сумма весов которого равна t. Рекуррентное соотношение будет следующим:

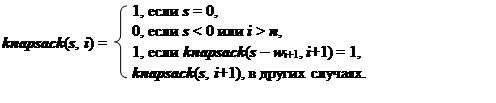
Напишем подпрограмму, соответствующую этому соотношению. Учитывая, что индексы массива принимают значения от 0, обозначим w[i] = w_i+1. Массив весов теперь будет состоять из чисел w[0], …, w[n-1]. Обозначим первый аргумент подпрограммы через t, а второй – через cand. Получим подпрограмму

int knapsack( int t, int cand )

{

if (t == 0) return 1;

if (t < 0 || cand >= n) return 0;

else if (knapsack(t-w[cand],cand+1))

{

printf(" %d",w[cand]);   // выводим число, вычтенное из t

return 1;

}

else return (knapsack( t,cand+1 ));

}

Теперь для тестирования этой подпрограммы надо определить массив весов w[ ] и количество весов n. Рассмотрим случаи t = 32 и t = 28, веса равны: 6, 8, 8, 11, 12. Окончательное решение будет следующим:

// Задача о ранце

#include <stdio.h>

#include <math.h>

#include <conio.h>

int w[ ] = {6, 8, 8, 11, 12};

int n;

int knapsack( int t, int cand )

{

if (t == 0) return 1;

if (t < 0 || cand >= n) return 0;

else if (knapsack(t-w[cand],cand+1))

{

printf(" %d",w[cand]);   // выводим число, вычтенное из t

return 1;

}

else return (knapsack( t,cand+1 ));

}

main()

{

clrscr();

n=5; // количество весов – элементов множества w[ ]

if (knapsack(12+12+8,0))printf("\n");