Использование алгоритма генерации точек отрезка, вывд на экран треугольника и, использование алгоритма заполнения

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 2

Задание 1. Используя алгоритм генерации точек отрезка, вывести на экран треугольник и, используя алгоритм заполнения, закрасить его.

Варианты заданий. Генерация точек границы треугольника производится по одному из следующих алгоритмов:

L1. Симметричный ЦДА.

L2. Простой ЦДА.

L3. Алгоритм Брезенхема.

L4. Метод приращений.

L5. Метод приращений, использующий четыре перемещения.

Область закрашивается с использованием одного из следующих алгоритмов:

F1. С запоминанием точек границы в стек.

F2. С установкой режима XOR_PUT.

F3. Построчный алгоритм заполнения с затравкой.

F4. Построчный алгоритм с затравкой с использованием рекурсии.

F5. Простой алгоритм заполнения с затравкой с использованием рекурсии.

F6. Простой алгоритм заполнения с затравкой.

Комбинации этих алгоритмов распределяются между вариантами 01-25 так:

Для всех вариантов, кроме 05-09 рекомендуется в качестве изображения выбирать не пиксел, а закрашенный квадрат со стороной в несколько пикселов.

Задание 2. Построить алгоритм для генерации точек указанной кривой, принадлежащих данной четверти.

Варианты заданий.

1)   x2 + y2 = R2,                I	8)     y = ax2, a > 0,                                       II		15)   y = ax3, a < 0,       II
2)   y = ax2, a > 0,              I	9)     y= ax3, a > 0,                                      III		16)   a2x3 - y2 = 0,          I
3)   y = ax3, a > 0,              I	10)   x2 / a2 - y2 / b2 = 1,                                       II		17)   x2/a2 - y2/b2 = 1,                                     III
4)   x2 / a2 - y2 / b2 = 1,        I	11)   y2= 2px, p > 0,                                      IV		18)   x2 + y2 = R2,                                     III
5)   y2 = 2px, p > 0,            I	12)   ay3 – x = 0, a > 0,    I		19)   y= ax2, a < 0,                                     IV
6)   x2 + y2 = R2,                 II	13)   x2 + y2 = R2,                                      IV		20)   y = ax3, a < 0,                                     III
7)   ay3 - x = 0, a > 0,                                         IV	14)   y = ax2, a < 0,                                      III		21)   a2x3 - y2 = 0,                                     IV
22)   x2 / a2 - y2 / b2 = 1,           IV		24)   ay3 – x = 0, a > 0,                       III
23)   x2 / a2 + y2 / b2 = 1,          IV		25)   ay3 – x = 0, a < 0,                       IV

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 1

Задание. Используя алгоритм Брезенхема, вывести на экран треугольник и, используя алгоритм закраски с запоминанием точек границы в стек, закрасить его.

Решение. Ниже мы  рассмотрим реализацию, при которой стек представляется  в виде  массива. За основу возьмем пример 2.1.

Программа

#include <conio.h>

#include <graphics.h>

#include <math.h>

#define pop() stx[--deep]

#define push(x) stx[deep++]=x

/*Вывод горизонтального отрезка с

координатами начала (x0,y) и конца (x1,y)*/

void horline (int y, int x0, int x1)

{

int i;

if (x0>x1) {i=x1; x1=x0; x0=i;}

for (i=x0; i<=x1; i++) putpixel (i, y,15 ) ;

}

//Вывод закрашенного многоугольника

//dimar - число вершин многоугольника

//arx - массив x координат вершин

//ary - массив y координат вершин

void fl(int *arx, int *ary, int dimar)

{

int deep=0;

int stx[1000];                      /*Стек в виде массива*/

int i0, iglob, ix0, iy0, ix1, iy1;

int ymin;

int ix, iy, deltax , deltay, esh, sx, sy;

int temp, swab, i;

i0=0; ymin=ary[0];

/*Находим вершину с наименьшей y координатой

ary[i]*/

for (i=0;i<dimar;i++)

if (ary[i]<ymin) {i0=i; ymin=ary[i];}

/*Вывод стороны многоугольника от вершины i к вершине i+1,

от (arx[i], ary[i]) до  (arx[i+1], ary[i+1])*/

iglob = i0 ;

do      {

ix0=arx[iglob]; iy0=ary[iglob];

iglob++; if (iglob==dimar) iglob=0;

ix1=arx[iglob]; iy1=ary[iglob];

//основной цикл - вывод отрезка – генерация точек отрезка по

//алгоритму Брезенхема

ix=ix0;

iy=iy0;

deltax=abs(ix1-ix0);    //dx

deltay=abs(iy1-iy0);    //dy

if (ix1-ix0>=0) sx=1; else sx=-1;

if (iy1-iy0>=0) sy=1; else sy=-1;

//Если направление y главное, то перестановка dx и dy

if (deltay>deltax) {temp=deltax; deltax=deltay; deltay=temp; swab=1;}

else swab = 0;    //Былаперестановка

esh=2*deltay-deltax;      //E

for (i=1;i<=deltax;i++)

{

while (esh>=0)

{

if (swab==1) ix=ix+sx;

else

{

iy=iy+sy;

                        //При увеличении y на единицу, заносим

                        //в стек координату x предыдущей точки

if (sy==1) push (ix) ;

                        //При уменьшении y на единицу, извлекаем

                        //координату x из стека и проводим

                        //горизонтальный отрезок

if (sy==-1) {temp=pop(); horline(iy,ix,temp);}

}

esh=esh-2*deltax ;

}

if (swab==1)

{

iy=iy+sy;

if (sy==1) push(ix);

if (sy==-1)

{

temp=pop();

horline(iy,ix,temp);

}

}

else ix=ix+sx;

esh=esh+2*deltay;

}

      //Пока не рассмотрены все вершины многоугольника

} while (i0!=iglob) ;

}

void main()

{

int gd=DETECT,gm;

int arx[3]={200,250,100}; //x координатывыводимоготреугольника

int ary[3]={120,180,60}; //y координаты выводимого треугольника

initgraph(&gd,&gm,""); //Инициализация графического режима

/*Вызов функции fl, которая выводит стороны многоугольника

используя алгоритм Брезенхема, и закрашивает многоугольник,

используя алгоритм с запоминанием точек границы в стек*/

fl(arx,ary,3);

getch();

closegraph();   //Выход из графического режима

}

Результат работы программы

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 2

Задание. Построить алгоритм для генерации точек эллипса во второй четверти методом приращений.

Решение. Для выполнения этого задания будем опираться на пример, изложенный в п.п. 2.3 данного пособия.

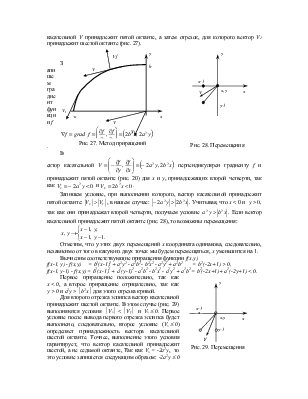
Уравнение эллипса 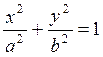 запишем в виде . В качестве начальной точки в нашем случае можно выбрать точку (0, b) или (-a, 0). Выбираем точку x₀ = 0, y₀ = b. Направление движения вдоль кривой – против часовой стрелки. В этом случае сначала выводится отрезок кривой, для которого вектор касательной V принадлежит пятой октанте, а затем отрезок, для которого вектор V₁ принадлежит шестой октанте (рис. 27).

Запишем градиент функции f

.

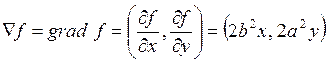Вектор касательной 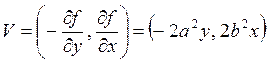 перпендикулярен градиенту f и принадлежит пятой октанте (рис. 20) для x и y, принадлежащих второй четверти, так как и .

Запишем условие, при выполнении которого, вектор касательной принадлежит пятой октанте: , в нашем случае: . Учитывая, что x < 0 и  y > 0, так как они принадлежат второй четверти, получаем условие . Если вектор касательной принадлежит пятой октанте (рис. 28), то возможны перемещения:

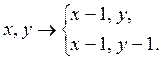
Отметим, что у этих двух перемещений x координата одинакова, следовательно, независимо от того в какую из двух точек мы будем перемещаться, x уменьшится на 1.

Вычислим соответствующие приращения функции f(x,y)

f(x-1, y) - f(x,y)     = b²(x-1)² + a²y² - a²b² - b²x² - a²y² + a²b²      =  b²(-2x+1) > 0,

f(x-1, y-1) - f(x,y) = b²(x-1)² + a²(y-1)² - a²b² - b²x² - a²y² + a²b² = b²(-2x+1)+ a²(-2y+1) < 0.

Первое приращение положительно, так как x < 0, а второе приращение отрицательно, так как y > 0 и a²y > ½b²x½ для этого отрезка кривой.

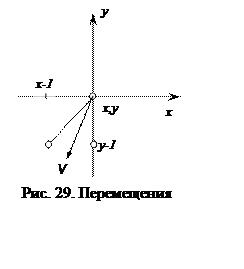
Для второго отрезка эллипса вектор касательной принадлежит шестой октанте. В этом случае (рис. 29) выполняются условия ½V_x½ < ½V_y½ и V_x £ 0. Первое условие после вывода первого отрезка эллипса будет выполнено, следовательно, второе условие (V_x £ 0) определяет принадлежность вектора касательной шестой октанте. Точнее, выполнение этого условия гарантирует, что вектор касательной принадлежит шестой, а не седьмой октанте, Так как V_x = -2a²y,  то это условие запишется следующим образом: -2a²y £ 0 или y ³0.

Так как вектор касательной принадлежит шестой октанте