Емкостные коэффициенты образуют симметричную матрицу. Энергия электрического поля в линейных диэлектриках

диэлектрической проницаемости ε в ряд Тейлора по степеням плотности среды τ:

                             FH ∂εI ² F^G_H ∂²εI^JKTT                    F_H ∂εIK

 ε τ≈1+         ⋅     KT +  ⋅τ ⋅              +...             => ε τ−1≈  ⋅          

                                             ∂τ 2             ∂τ                                          ∂τ _T

Факультатив. Другое выражение сил в диэлектриках.

          Покажем, что первое слагаемое в выражении

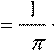
F^GH^FH ∂ε^IK T 2^IJK E² a f  fgrad τ⋅ E − ⋅ grad ε

                          8                ∂τ               8π

          эквивалентно давлению разному в разных точках диэлектрика.

--------

Рассмотрим среду, давление P в разных точках которой различно. Покажем, что это давление эквивалентно объемной плотности сил  f = −gradaPf.

Рассмотрим маленький куб с ребрами, направленными вдоль осей координат.

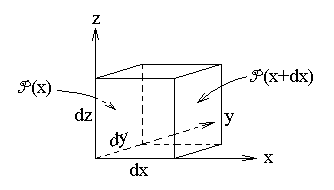
Рассмотрим давление на две грани перпендикулярные оси x. Площадь каждой грани равна dy⋅dz. X-координаты граней равны x и x+dx. Сумма сил, действующих на эти грани со стороны давления, определяет x-проекцию силы, действующей на куб:

∂P

          F_x = Paxf⋅dy dz⋅ − Pax + dxf⋅dy dz⋅ = −   ⋅dx dy dz⋅ ⋅  

∂x   Объемная плотность x-проекции силы:

∂P

                               x       −       ⋅dx dy dz⋅          ⋅        ∂P

            fx = F =     ∂x                  = −                   =>

                            V           dx dy dz⋅               ⋅        ∂x

            f = −∇P, что и требовалось доказать.

--------

          Тогда первое слагаемое

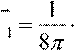∂εI

       fgradF^GHFH K τ⋅ E²I^JK

∂τ _T

          в    выражении     f      1   _gradF^G_HF_H ∂εIK Tτ⋅ E²I^JK ^{− E2} ⋅ _grada fε                   эквивалентно

                                                                     8                 ∂τ               8π

давлению

                                 1        ²F ∂εI

          ^P₁ = − ⋅τ⋅ E H K ,

                               8π           ∂τ _T

которое никуда не втягивает диэлектрик и для несжимаемого диэлектрика может быть отброшено. И действительно, если диэлектрик сдавить, то упругие силы в диэлектрике уравновесят давление. Следовательно, сила f₁ только растягивает P₁ < 0 диэлектрик, но никуда его не втягивает.

Если диэлектрик несжимаемый (жидкий или твердый), то силу f₁ можно не учитывать. В таком случае можно считать. что на диэлектрик действует только сила f₂ :

         f      .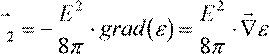

--------

Силу f₂ можно заменить эквивалентным давлением P₂ , приложенным к границам диэлектрика, если диэлектрик однородный и несжимаемый. Обсудим это подробнее.

Если диэлектрик однородный, то ∇ =ε 0. Следовательно, f₂ = 0 везде, кроме границ диэлектрика, где ε испытывает скачок.

∂ε

На границе диэлектрика    = ∞, отсюда следует, что ∇ε направлен ∂n

перпендикулярно границе диэлектрика, ∇ = ∞ε и f₂ = ∞. Бесконечно большая объемная плотность сил в бесконечно тонком поверхностном слое диэлектрика эквивалентна давлению на границу диэлектрика.

          Найдем это давление.

Рассмотрим малый участок границы диэлектрика. Направим ось z перпендикулярно границе. Градиент диэлектрической проницаемости ∇ε и объемная плотность сил f₂ также будут перпендикулярны границе.

          Рассмотрим границу диэлектрика, как переходный слой конечной толщины h . Если ось z направлена из объема 1 в объем 2, то z f_2z ⋅dV   z f_2z ⋅S dz⋅

           P21 2→ = F2z = V                     = V                    = z f dz2z        =

                                    S            S                  S            _V

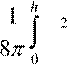
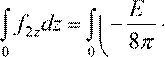              =    F   _grada fεI^JK ⋅dz = −       E ⋅b_grada fεgz ⋅dz = h           h             2

z

           =                      .

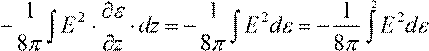
Зависимость подынтегрального выражения от диэлектрической проницаемости ε можно найти с учетом того, что при переходе через границу диэлектрика сохраняется тангенциальная составляющая поля E_τ, так как E₂τ− E₁τ = 0, и сохраняется нормальная составляющая поля D_n , так как

D_2n − D_1n = 4πσ= 0. На границе нет свободных зарядов σ= 0. Тогда

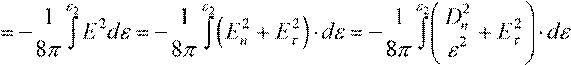                              P21 2→                           . ε1           ε1               ε1

  Интеграл может быть разбит на сумму двух интегралов. Величины D_n и

E_τ не изменяются внутри переходного слоя границы диэлектрика и могут быть вынесены за пределы соответствующих интегралов. Тогда

           P21 2→ .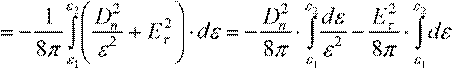

          Окончательно получаем:

  P21 2→ = D8π ε ε πn2  12 − 11  + E8τ2 (ε ε1 − 2).

Это давление приложено к границе двух диэлектриков и направлено в сторону диэлектрика с меньшей диэлектрической проницаемостью.

--------

Рассмотрим втягивание жидкого диэлектрика в заряженный конденсатор, считая, что есть только сила f₂ .

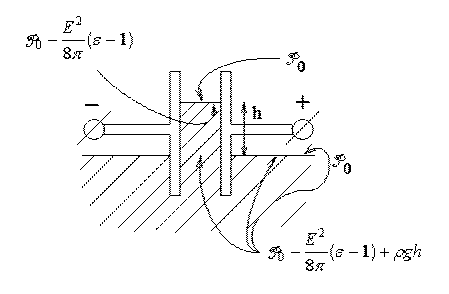
Пусть атмосферное давление равно ^P₀ . На границе диэлектрика внутри заряженного конденсатора есть только тангенциальная составляющая напряженности электрического поля E_τ = E . В таком случае к границе

                                                                                                    E2 a   f

диэлектрика приложено давление ^P₂ = ε−1 , которое тянет диэлектрик за 8π

его верхнюю границу вверх. В таком случае под границей диэлектрика давление меньше атмосферного на величину P₂ . Под границей жидкого диэлектрика давление растет с глубиной h , как ρgh. Если h — высота подъема диэлектрика в конденсаторе, то внутри конденсатора давление на глубине h равно давлению снаружи конденсатора на той же высоте и равно ^P₀ ^{− E2} aε ρ−1f+ gh. Это давление снаружи конденсатора будет как под 8π

границей диэлектрика, так и над его границей. Электрического поля снаружи конденсатора почти нет, поэтому нет и электрического давления на поверхность жидкости. То есть давление над поверхностью тоже

0          E2 a   f

P − ε ρ−1 + gh, но с другой стороны — это атмосферное давление