








![]()
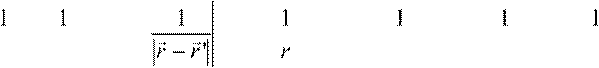
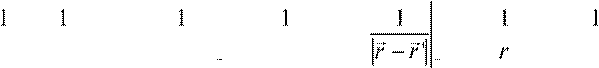
![]()
![]()
![]() 1 1
FGHr ' 0IJK 1
F0I 1
F 1IK
1 1
FGHr ' 0IJK 1
F0I 1
F 1IK
![]() ≈ + r',∇'= − GHr',∇r ' JK = − Hr',∇ r − r' rrr r
≈ + r',∇'= − GHr',∇r ' JK = − Hr',∇ r − r' rrr r
![]()
![]()
![]() ==
q
==
q
r
![]() Здесь ∇1 = − r3 , так как E q
Здесь ∇1 = − r3 , так как E q ![]() r3 . Тогда
r rr
r3 . Тогда
r rr
|E = −∇ϕ T|
![]()
![]() 1 ≈ 1 − FHr',− r3 IK = 1 + 13 ⋅ar r', f
r − r' r r r r
1 ≈ 1 − FHr',− r3 IK = 1 + 13 ⋅ar r', f
r − r' r r r r
Подставим это в выражение для векторного потенциала контура с током
A ra f = z I ⋅ dr' и получим l' c r − r'
![]() A ra f = I ⋅z dr' ≈ I ⋅TRSzl' dr' +
zl' ar r',3 fdr'UWV = I ⋅ 1⋅zl' dr'+
I ⋅ 13 ⋅zar r dr', f '
c l' r − r' c r r c
r c r l'
A ra f = I ⋅z dr' ≈ I ⋅TRSzl' dr' +
zl' ar r',3 fdr'UWV = I ⋅ 1⋅zl' dr'+
I ⋅ 13 ⋅zar r dr', f '
c l' r − r' c r r c
r c r l'
![]() Здесь первый интеграл
в правой части равенства равен нулю zdr' = 0, так как интеграл zda⋅ =f 0
равен нулю для любой функции под знаком l'
Здесь первый интеграл
в правой части равенства равен нулю zdr' = 0, так как интеграл zda⋅ =f 0
равен нулю для любой функции под знаком l'
l'
дифференциала и в частности для r '. Тогда
I
![]() A ra f
A ra f![]() zar
r dr', f '
zar
r dr', f '
cr l'
Мы
хотим выразить векторный потенциал A ra f через магнитный дипольный момент m ≡ ![]() I S , где S —
вектор площадки ограниченной контуром c
I S , где S —
вектор площадки ограниченной контуром c
с током I .
С этой целью рассмотрим
![]()
![]()
![]()
![]() m B, = M = zdM
= z r
dF', ' = zLMNr',
I dl ',B
m B, = M = zdM
= z r
dF', ' = zLMNr',
I dl ',B![]() OPQ
OPQ
l' l' l' c
Здесь в последнем равенстве подставлено выражение для силы Ампера
dF = ![]() I dl ',B , действующей на
элемент тока Idl ', радиус-вектор которого c
I dl ',B , действующей на
элемент тока Idl ', радиус-вектор которого c
равен r '.
![]()
![]() Учтем, что dl '= dr', и
получим m B, = zLMNr',
I dr B',
OPQ = I ⋅z r',
dr B',
Учтем, что dl '= dr', и
получим m B, = zLMNr',
I dr B',
OPQ = I ⋅z r',
dr B', ![]() .
.
l' c c l'
Двойное векторное произведение в правой части равенства преобразуем по правилу "бац минус цап" и получим
![]()
![]()
![]()
![]() m B, = I ⋅zdr
r B'c
', h− I ⋅z B
r dra
', 'f
= I ⋅zcr
B dr', h '
− I B⋅zar
dr', 'f
m B, = I ⋅zdr
r B'c
', h− I ⋅z B
r dra
', 'f
= I ⋅zcr
B dr', h '
− I B⋅zar
dr', 'f
c l' c l' c l' c l'
![]() Второй
интеграл в правой части равенства равен нулю. И действительно, d r ra ',
'f
=
adr
r', 'f+
ar
dr', 'f
= 2ar
dr', 'f
=> ar
dr', 'f
=
Второй
интеграл в правой части равенства равен нулю. И действительно, d r ra ',
'f
=
adr
r', 'f+
ar
dr', 'f
= 2ar
dr', 'f
=> ar
dr', 'f
= ![]() d
r ra
', 'f
=> zar
dr', 'f
= 1 ⋅zd
r ra
', 'f,
где последний интеграл равен нулю, так как интеграл
d
r ra
', 'f
=> zar
dr', 'f
= 1 ⋅zd
r ra
', 'f,
где последний интеграл равен нулю, так как интеграл
![]() l'2 l' zda⋅ =f 0
равен нулю для любой функции под знаком дифференциала.
l'2 l' zda⋅ =f 0
равен нулю для любой функции под знаком дифференциала.
l'
![]() Тогда в
выражении для векторного произведения m B, останется только первый
интеграл:
Тогда в
выражении для векторного произведения m B, останется только первый
интеграл:
![]() m
B, =
I ⋅zcr
B dr', h '
m
B, =
I ⋅zcr
B dr', h '
c l'
Это равенство справедливо для любого значения вектора B, если считать, что поле B одинаковое во всех точках.
![]()
![]() Хотя это равенство было
получено с использованием закона Ампера dF = I dl B, , вектор B
в равенстве m B, = I ⋅zcr
B dr', h
' может иметь любое c c l'
Хотя это равенство было
получено с использованием закона Ампера dF = I dl B, , вектор B
в равенстве m B, = I ⋅zcr
B dr', h
' может иметь любое c c l'
значение, а значит, его можно сделать равным любому наперед заданному вектору, например, вектору r .
![]() Следовательно, в
равенстве m B, = I ⋅zcr
B dr', h '
вектор B можно
Следовательно, в
равенстве m B, = I ⋅zcr
B dr', h '
вектор B можно
c l'
![]() заменить на
вектор r . В результате получим m r, =
I ⋅zar
r dr', f
'.
заменить на
вектор r . В результате получим m r, =
I ⋅zar
r dr', f
'.
c l'
![]() Сравним это
равенство с полученным выражением для векторного потенциала A ra fzar
r dr', f
' и получим
Сравним это
равенство с полученным выражением для векторного потенциала A ra fzar
r dr', f
' и получим
I
cr l'
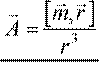 —
векторный потенциал точечного магнитного диполя, где r
—
векторный потенциал точечного магнитного диполя, где r
— вектор из диполя в точку наблюдения. Формулу без доказательства нужно знать к экзамену.
Заметим, что это равенство похоже на потенциал электрического диполя ϕ= ap r,3 f .
r
Факультатив. Магнитное поле B точечного магнитного диполя.
Правую часть равенства распишем по правилу "бац минус цап" и получим
![]() B
= mFH∇, r3 IK − r3 d∇,mi.
r r
B
= mFH∇, r3 IK − r3 d∇,mi.
r r
Первое слагаемое в правой части равенства равно нулю, так как
FH∇, ![]() r3 IK = divFH
r3 IK = divFH ![]() r3 IK = div Ec 1h,
где E1 — напряженность поля единичного r r
r3 IK = div Ec 1h,
где E1 — напряженность поля единичного r r
точечного заряда в начале координат, в точке r = 0. По теореме Гаусса в дифференциальной форме div Ec h = 4πρ, а для единичного точечного заряда в начале координат имеем ρ= 0 во всех точках кроме точки r = 0,
следовательно, div Ec h = 0 во всех точках, кроме
точки r = 0,
тогда и FH∇, ![]() r3 IK = 0 r во всех
точках, кроме точки r =
0.
r3 IK = 0 r во всех
точках, кроме точки r =
0.
Тогда магнитное поле диполя:
B =
−dm,∇i ![]() r3 .
r3 .
r
Раскроем правую часть равенства, как производную от произведения r на
1
![]() :
:
r 3
![]() B
= −
B
= − ![]() 13 dm,∇ir
− r md ,∇i 13 = − 13 dm,∇ir
− r mFH ,∇
13 dm,∇ir
− r md ,∇i 13 = − 13 dm,∇ir
− r mFH ,∇ ![]() 13 IK .
r r r r
13 IK .
r r r r
Рассмотрим подробнее первое слагаемое правой части равенства: dm,∇ =ir FGHmx ∂∂x + my ∂∂y + mz ∂∂zIJKdxi + +yj zki= mx ∂∂x xi + my ∂∂y yj + mz ∂∂z zk = m ix + m jy + m kz = m
Тогда
B =
− ![]() m3 − r mFH ,∇
m3 − r mFH ,∇ ![]() 13 IK .
r r
13 IK .
r r
Рассмотрим теперь второе слагаемое:
![]() ∇FH
∇FH ![]() 13 IK = ∇FGHFH
13 IK = ∇FGHFH![]() 1IK 3IKJ = 3FH1IK 2 ∇1 .
1IK 3IKJ = 3FH1IK 2 ∇1 .
r r r r
![]() Здесь ∇1 = − r3 , так как |SE
= q
Здесь ∇1 = − r3 , так как |SE
= q ![]() r3 . Тогда
r r | r
r3 . Тогда
r r | r
|E = −∇ϕ
∇FH ![]() 13 IK = 3⋅FH
13 IK = 3⋅FH ![]() 12 IK ⋅ −FH
12 IK ⋅ −FH ![]() r3 IK = −3
r3 IK = −3 ![]() r5 .
Подставим это значение в выражение для r r r r магнитного
поля B точечного магнитного диполя и полуим:
r5 .
Подставим это значение в выражение для r r r r магнитного
поля B точечного магнитного диполя и полуим:
B =
− ![]() m3 − r mFH ,−3
m3 − r mFH ,−3 ![]() r3 IK = 3am
r r, 5 f −
r3 IK = 3am
r r, 5 f − ![]() m3 . r r r r
m3 . r r r r
B =
3am r r, 5 f − m3 —
магнитное поле точечного диполя, где m ≡
![]() I S —
I S — ![]() c магнитный
дипольный момент, r — вектор из диполя в точку наблюдения. Эту формулу
без доказательства нужно знать к экзамену. Заметим, что это выражение полностью
совпадает с выражением для электрического поля,
c магнитный
дипольный момент, r — вектор из диполя в точку наблюдения. Эту формулу
без доказательства нужно знать к экзамену. Заметим, что это выражение полностью
совпадает с выражением для электрического поля,
![]() создаваемого
электрическим диполем E =
3ap r r, 5 f −
создаваемого
электрическим диполем E =
3ap r r, 5 f − ![]() p3 . a f a f r r
p3 . a f a f r r
B ![]() m r
магнитное поле точечного диполя с учетом r r 3
m r
магнитное поле точечного диполя с учетом r r 3
![]() поля внутри
самого диполя (без доказательства). Но a f
поля внутри
самого диполя (без доказательства). Но a f
E ![]() p arf.
p arf.
r r 3
Магнитное поле в веществе.
Экзамен. Намагниченность и связанные токи.
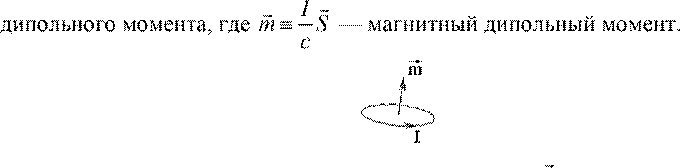
M ≡ ![]() dm — намагниченность
или объемная плотность магнитного dV
dm — намагниченность
или объемная плотность магнитного dV
Для
электрического поля аналогично P ≡
![]() dp — поляризация или
dV
dp — поляризация или
dV
объемная плотность электрического дипольного момента
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.