Электрический диполь. Потенциал поля точечного диполя. Изменение дипольного момента при переходе от одной системы отсчета к другой

Изменение дипольного момента при переходе от одной системы отсчета к другой.

Пусть r_I→II — положение второй системы отсчета относительно первой, r_I→i — радиус-вектор заряда q_i в первой системе отсчета, r_II→i — радиусвектор заряда q_i во второй системе отсчета.

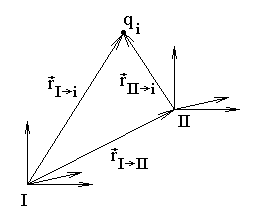
Из рисунка видно, что r_II→i = r_I→i − r_I→II . Обозначим дипольный момент относительно первой системы отсчета за p_I , а относительно второй системы —

p_II . Тогда

       pII = ∑q ri II→i = ∑qi ⋅brI→i − rI→II g = ∑q ri I→i − FHG∑qiIJK ⋅rI→II = pI − Q r⋅ I→II

i i i i

 pII = pI − Q r⋅ I→II

Здесь p_II — дипольный момент во второй системе отсчета, p_I — дипольный момент в первой системе отсчета, Q — полный заряд системы, r_I→II — положение второй системы отсчета относительно первой.

Экзамен. p_II = p_I при Q = 0.

Дипольный момент не зависит от системы координат, если полный заряд системы равен нулю. Обычно дипольный момент системы зарядов рассматривают только в том случае, если полный заряд системы равен нулю. Тогда обычно величина дипольного момента не зависит от положения начала координат.

Экзамен. Простейший электрический диполь.

Простейший электрический диполь — это пара точечных зарядов противоположных знаков и одинаковых по модулю.

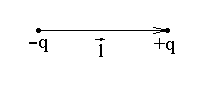
            p q r      ql       =>

i

           p = ql

Здесь p — дипольный момент пары зарядов −q и +q , l — вектор направленный из заряда −q к заряду +q .

Факультатив. Простейший квадруполь, октуполь, гексадекаполь и т.д.

Если точечный заряд продублировать, поменять знак и сдвинуть, то полученная пара зарядов образует простейший диполь.

Если заряды простейшего диполя продублировать, поменять их знаки и сдвинуть на один и тот же вектор, то образуется простейший квадруполь.

          На рисунке приведены два варианта квадруполей.

Если заряды простейшего мультиполя продублировать, поменять их знаки и сдвинуть на один и тот же вектор, то образуется простейший мультиполь следующего порядка.

Экзамен. Напряженность поля точечного диполя.

ap r_, f

          E = −∇ϕ= −∇    ₃

r

       Раскроем последнее выражение, как производную от произведения ap r, f

1 на ₃ . r

                               ap r, f   1    a  f a  f   1₃

                         E = −∇  ₃             = − ₃ ⋅∇ p r,    − p r, ⋅∇      r     r         r

Вычислим отдельно каждую из производных в последнем выражении.          Сначала вычислим ∇ap r, f.

                 ∂              ∂

        ap r, f = dp x_x + p y_y + p z_z i = p_x      =>            ∇ap r, f = p

               ∂x             ∂x

1

          Вычислим теперь ^∇ ₃ . r       ∇ 3 = ∇FGHFH IK3IJK = 3FH IK2 ⋅∇       

                      1            1             1         1

                     r             r              r          r

1

  Найдем ∇ : r q U| ϕ=

                          r     |

                      1      F1I   1     F1I F  r I     r

              ∇ 3 = 3H K ⋅∇        = 3H K ⋅ −H 3K = −3 5 . r r       r         r         r         r

^∇ap r^, f = p

                                           S                  13     a  f a  f   13

             Подставим 1              _r в E = −      ⋅∇ p r,   − p r,  ⋅∇ и получим:

_T|∇ ₃ = −3 ₅             r         r r     r

                         ap r r, f  p

         ₅     , где r — вектор, направленный из диполя p в точку наблюдения.

Факультатив. Напряженность поля точечного диполя с учетом поля внутри самого диполя.       Без доказательства: a f

           E                      p    arf.

                                   r          r      3

Здесь ^δarf — дельта-функция Дирака. Для дельта-функции по определению: при r ≠ 0: δarf = 0,  при r =0: δarf = ∞,  z_δarf⋅dV =1.

          f — очень узкая и очень высокая функция.

Для точечного заряда q₀, расположенного в точке r₀, объемная плотность заряда:  ρarf = q₀ ⋅δbr − r₀g.

Экзамен. Момент сил, действующих на точечный диполь в электрическом поле.

         Рассмотрим систему зарядов lq_iq, близко расположенных друг к другу.

Суммарный момент внутренних сил равен нулю в соответствии с третьим законом Ньютона. Тогда момент сил, действующих на систему зарядов, можно найти, как сумму моментов внешних сил, действующих на каждый из зарядов:

         M = ∑ M_i = ∑ r F_i , _i = ∑r q E_i , _{i       i}  .

                              i                   i                         i

Если расстояния между зарядами малы, то напряженности внешнего электрического поля в точках расположения разных зарядов примерно равны

E_i ≈ E . => L O

         M = ∑ r q E_i , _{i i} ≈ ∑r q E_i , _i= ∑q r E_{i i} ,= _NM∑q r E_{i i} , _QP = p E,                                                         =>

                              i                              i                             i                               i

            M = p E,     , где M — момент сил, p — дипольный момент, E — внешнее по отношению к диполю электрическое поле.

Экзамен. Сила, действующая на точечный диполь в электрическом поле.

Сумма внутренних сил между зарядами диполя равна нулю по третьему закону Ньютона. Тогда силу, действующую на диполь, можно найти, как сумму внешних сил, действующих на отдельные заряды диполя:

           F = ∑F_i = ∑qE_{i i} .

                            i                i

Если, как и в предыдущем вопросе считать, что E_i ≈ E , то для диполя с нулевым суммарным зарядом суммарная сила будет равна нулю. В таком случае для определения величины силы потребуется учесть небольшое различие величин E_i в точках расположения разных зарядов диполя. Чтобы учесть это различие, разложим напряженность электрического поля E в ряд Тейлора в малой окрестности рассматриваемого диполя.

          Поместим начало координат вблизи зарядов диполя. Рассмотрим разложение x-проекции поля E в ряд Тейлора в точке расположения заряда q_i . Это разложение по степеням радиус-вектора r_i . По аналогии с одномерным рядом Тейлора:

|f xa f ≈ _f a f0 _{+ x⋅}U| df |^|S i dx x=0^||V | | T^||f xa f→ E_ix = E r_xb g_i W^||

             x → r                                     =>

  E_ix = E r_xb _i g ≈ E_xa0f + ^FHr_i ,∇E_x r=0^IK = E_x ⁺dr_i ,∇E_x i = E_x ⁺dr_i ,^∇iE_x                                                                                               =>

i

         E_i ≈ E +dr_i ,∇iE            =>

            F = ∑ ∑q E_{i                                     i} ≈       q E_io + dr_i ,∇iEt = E ⋅∑ ∑q_i + F^GH q r_{i i} ,∇I^JKE = QE + dp,∇iE

                            i                     i                                                        i                   i

В последнем выражении первое слагаемое — сила, действующая на полный