Оператор любой физической величины и среднее значение любой физической величины. Уравнение Шредингера

Оператор любой физической величины и среднее значение любой физической величины.

Произвольная физическая величина, которая зависит от состояния электрона, может быть выражена через его координаты и импульс.

Рассмотрим сначала физическую величину F , которая зависит только от координат электрона F r( ).

По определению вероятности p_i i -го состояния среднее значение физической величины F можно найти по формуле:

            F =∑ p Fi i ,

i

           где F_i — значение физической величины F в i -ом состоянии.

 Вероятность найти электрон в малом объеме dV выражается через квадрат модуля волновой функции и равна Ψ ² dV . Тогда, суммируя по всем объемам dV , в которых может оказаться электрон, получим равенство, которое справедливо в каждый момент времени:

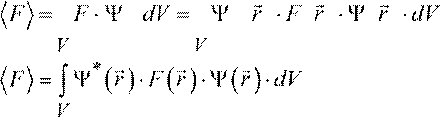
                 ∫ F ⋅ Ψ ² dV ⁼ ∫ Ψ^*( )r ⋅ F r( )⋅Ψ( )r ⋅dV           =>

                              r     F r          r    dV                                       (2.1)

Рассмотрим теперь физическую величину, которая произвольным образом зависит только от импульса электрона F p( ). Для плоской волны

i

( p r Et, − )

Ψ = Ae^ℏ с определенным значением импульса можно p написать равенство

          F p F p    t r       F p     t r                                          dV ,

V

так как F p( ) в правой части равенства можно вынести за знак интеграла, а оставшийся интеграл равен единице, поскольку представляет собой сумму всех вероятностей обнаружить электрон в разных объемах dV .

Это равенство справедливо для любого значения импульса и соответствующей плоской волны Ψ.

              Если в правую часть равенства вместо F p( ) подставить ту же функцию

F только от оператора импульса −iℏ∇ , а не от самого импульса p , то равенство сохранит смысл. Функцию от оператора F(−iℏ^∇) нужно понимать следующим образом. Нужно взять разложение в ряд Тейлора функции F p( ) по степеням импульса p , и в этом разложении заменить импульс на оператор импульса −iℏ∇ . Считая, что ∇² = ∆ , можно осмыслить любую степень оператора импульса. В таком случае каждое слагаемое ряда из операторов имеет смысл, и весь ряд имеет смысл функции F от оператора импульса.

Если рассмотреть действие функции F от оператора импульса на плоскую волну с определенным значением импульса, то надо рассмотреть действие ряда Тейлора по степеням оператора импульса на эту волну. Каждое слагаемое ряда после воздействия на волну даст ту же самую волну только с сомножителем в виде импульса в соответствующей степени. При сложении ряда получиться та же самая волна только с сомножителем F p( ).

       Тогда в правой части равенства F p                                                                t r                      F p     t r    dV для

V

полоской волны Ψ с определенным значением импульса вместо сомножителя F p( ) можно поставить функцию от оператора импульса F(−iℏ^∇). Результат при этом не изменится. Тогда можно записать новое равенство

          F p t r           F        i           t r                                       dV                  (2.2)

V

i

( p r Et, − )

для плоской волны Ψ = Ae^ℏ с определенным значением импульса p .

Равенство (2.2) будет справедливо и для произвольной локализованной функции Ψ, у которой нет определенного значения импульса, так как эту функцию можно в двух местах правой части равенства разложить по плоским волнам.

И действительно. Оператор F(−iℏ^∇), действующий на каждую из плоских волн, будет давать ту же плоскую волну с коэффициентом F p( ). Если комплексно сопряженный сомножитель Ψ^*_p — другая плоская волна, то интеграл равен нулю, так как плоские волны ортогональны, и равен нулю интеграл от любых двух разных плоских волн .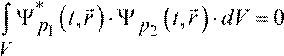

Следовательно, в правой части равенства (2.2) при разложении функции Ψ по плоским волнам останутся только слагаемые, в которых Ψ^*_p и ^Ψ _p — плоская волна с одним и тем же импульсом. Для этой плоской волны с определенным импульсом p интеграл 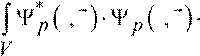t r t r dV представляет собой вероятность конкретного значения импульса p в исходной локализованной функции Ψ равенства (2.2).

  Следовательно, в правой части равенства (2.2) получается сумма вида

∑ p F_{i i} , которая по определению вероятности p_i и равна среднему значению i

F p( ) . Таким образом, равенство (2.2) оказывается справедливым для произвольной локализованной функции