Здесь во второй формуле имеет место параметр p, который связан со статистикой возбуждения верхнего лазерного уровня. Если накачка совершенно случайная (пуассоновская), то p = 0, если - строго регулярная (субпуассоновская), то p = 1. Промежуточные ситуации характеризуется соотношением 0 < p < 1, а суперпуассоновская накачка имеет место при p < 0.
Для построения спектров фототока при детектировании лазерного излучения нам важно будет знать еще средние от нормально упорядоченных произведений операторов. Они также могут быть найдены в работах
[3, 4]:
h: Fˆ1(t)Fˆ1(t0) :i =
h i
= γ1hN1i − ghaˆ†Pˆ + aˆPˆ†i + R(1 − p) δ(t − t0), (4.22) h i
h: Fˆ2(t)Fˆ2(t0) :i = γ2hN2i − ghaˆ†Pˆ + aˆPˆ†i δ(t − t0), (4.23) h: Fˆ1(t)Fˆ2(t0) :i = ghaˆ†Pˆ + aˆPˆ†i δ(t − t0), (4.24) h: Fˆp†(t)Fˆp(t0) :i =
= h: Fˆp(t)Fˆp†(t0) :i = [ (2γ⊥ − γ1)hN1i + R ] δ(t − t0), (4.25) h: Fˆp(t)Fˆp(t0) :i = 2ghaˆPˆi δ(t − t0), (4.26) h: Fˆp(t)Fˆ2(t0) :i = h: Fˆ2(t)Fˆp(t0) :i = γ2hPˆi δ(t − t0). (4.27)
При том выборе атомных констант, который был нами сделан, мы можем понять, что среди прочих переменных поляризация лазерного перехода Pˆ и заселенность нижнего лазерного уровня Nˆ2 являются самыми быстрыми переменными, и они могут быть исключены из теории в рамках адиабатического приближения. Тогда из равенств Pˆ˙ = 0 и Nˆ˙ 2 = 0 можно в явном виде записать значения Pˆ и Nˆ2 как функции от aˆ и Nˆ1 и подставить их в оставшиеся два уравнения. Вследствие чего наша теория в адиабатическом приближении представляется теперь системой двух уравнений:
Nˆ˙ 1 = R − γ1Nˆ1 − caˆ†aˆNˆ1 + ξˆ1(t), c = 2g2/γ⊥ = β1γ1, (4.28) aˆ˙ = −C/2 aˆ + c/2 Nˆ1aˆ + ξˆa, (4.29) где новые источники выражаются через начальные в виде:
, (4.30)
ξˆa = Fˆa + g/γ⊥ (Fˆp − g/γ2 Fˆ2aˆ). (4.31)
Уравнение (4.29) легко линеаризуется, поскольку оно зависит только от числа атомов и числа фотонов, которые, разумеется, слабо флуктуируют около своих полуклассических значений:
|
εˆ= aˆ†aˆ − N ¿ N, δN1 = N1 − N1,cl. ¿ N1,cl.. После линеаризации получаем следующее: |
(4.32) |
|
δN˙ˆ1 = −Γ δNˆ1 − Cεˆ+ ξˆ1(t), Γ = γ1 + cN. |
(4.33) |
В то же самое время, линеаризовать уравнение (4.29), по меньшей мере, не просто. Дело в том, что из-за диффузии фазы поля, которая имеет место всегда в лазерной генерации, мы не можем, вообще говоря, потребовать, чтобы оператор
√
δaˆ = aˆ − N (4.34)
√
был бы много меньше величины N. В статистической полуклассической теории, где имеет место комплексная c-числовая амплитуда, мы
4.3. Адиабатические уравнения и их линеаризация могли бы перейти к двум переменным, а именно, к вещественной амплитуде поля и к фазе. При этом получается, что фазовое развитие оказывается независимым от амплитудного, что позволяет описать диффузию фазы, но одновременно провести линеаризацию по всем остальным переменным. В квантовой теории подобное представление оператора уничтожения фотонов оказывается затруднительным, поэтому затруднительно провести и корректную линеаризацию.
Частым подходом к этой проблеме является следующий. Дело в том, что скорость амплитудных (фотонных) и фазовых флуктуаций в лазерной системе существенно разные. Поскольку фазовые флуктуации обычно на много порядков более медленные, чем фотонные, то в наших уравнениях мы можем ограничить тот временной интервал, на котором процесс рассматривается, и пренебрегать фазовой диффузией в этом интервале. И тогда все-таки применить критерий малости комплексной амплитуды поля
√ √
δaˆ = aˆ − N ¿ N. (4.35)
Тогда мы сможем линеаризовать уравнение (4.29) в следующей форме:
δaˆ˙ = c/2N δNˆ1 + ξˆa. (4.36)
Перепишем это уравнение для комплексной амплитуды через квадратурные компоненты:
|
δaˆ = δXˆ + i δY .ˆ Нетрудно получить два следующих уравнения: |
(4.37) |
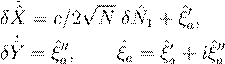(4.38)
. (4.39)
Теперь покажем, что δXˆ и εˆ это с точностью до коэффициента одно и тоже. Действительно,
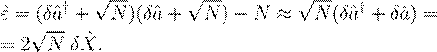(4.40)
Таким образом мы получаем систему из двух уравнений относительно двух переменных ε δˆ Nˆ1:
δN˙ˆ1 = −Γ δNˆ1 − Cεˆ+ ξˆ1(t), Γ = γ1 + cN, (4.41)
. (4.42)
Здесь стохастические источники выражаются через исходные в форме:
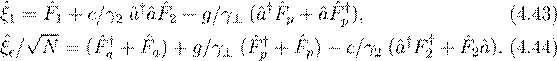
Теперь, что касается флуктуации другой квадратуры. Для малых флуктуаций мы можем отождествить эти флуктуации с фазовыми:
. (4.45)
Нетрудно увидеть, что флуктуации этой величины нарастают со временем неограниченно по закону диффузии hδY 2i = Dt. Но мы помним, что в наших приближениях мы имеем право рассматривать ситуацию, ограничиваясь достаточно малым временным интервалом t, пока диффузия фазы не успевает сказываться на движении других параметров.
Принимая во внимание соотношения между полуклассическими параметрами и корреляционные соотношения для исходных источников, можем получить ненулевые корреляционные функции в виде:
hξˆ²(t) ξˆ²(t0)i = N(C + cN1,cl.) δ(t − t0), (4.46) hξˆ1(t) ξˆ1(t0)i = ΓN1,cl.(2 − p) δ(t − t0), (4.47) hξˆ²(t) ξˆ1(t0)i = −cNN1,cl. δ(t − t0). (4.48)
И средние от нормально-упорядоченных операторов имеют вид:
h: ξˆ²(t)ξˆ²(t0) :i = 2cNN1,cl. δ(t − t0), (4.49) h: ξˆ1(t)ξˆ1(t0) :i = ΓN1,cl.(2 − p) δ(t − t0), (4.50) h: ξˆ²(t)ξˆ1(t0) :i = −2cNN1,cl. δ(t − t0). (4.51)
4.4. Спектральное представление уравнений
Далее нам удобно перейти на спектральный язык с помощью Фурьепреобразования, вводя вместо временной зависимостей частотную. Фурье преобразование, которое связывает функцию Λ(t) с ее спектральным образом Λω, дается интегральными соотношениями
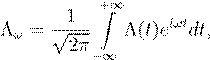
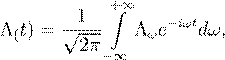(4.52)
Введем в рассмотрение спектральные плотности (ξ12)ω, (ξS2)ω и (ξ1ξS)ω как множители перед дельта-функциями в функциях корреляций:
hξˆ²ωξˆ²ω0i = (ξ²2)ω δ(ω + ω0), (4.53)
(4.54)
hξˆ²ωξˆ1ω0i = hξˆ1ωξˆ²ω0i = (ξ1ξ²)ω δ(ω + ω0). (4.55)
Принимая во внимание малость флуктуаций для числа атомов на верхнем лазерном уровне и для числа фотонов в резонаторе, учитывая стационарные полуклассические решения задачи, мы сможем записать спектральные мощности источников шума в следующем виде:
(ξ²2)ω = 2CN, (ξ12)ω = C/c Γ(2 − p),
(ξ1ξ²)ω = −CN. (4.56)
Аналогичным образом спектральные мощности для нормально упорядоченных величин даются формулами
(: ξ²2 :)ω = 2CN, (: ξ12 :)ω = C/c Γ(2 − p),
(: ξ1ξ² :)ω = −2Cn. (4.57)
Применим к уравнениям (4.41)-(4.42) фурье-преобразование, тогда получим следующую алгебраическую
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
