Резонансы двухфотонного поглощения без доплеровского уширения. Нестационарная нелинейная лазерная спектроскопия. Оптические уравнения Блоха

Резонансы двухфотонного поглощения без доплеровского уширения.

Как обычно поступают в нелинейной лазерной спектроскопии, рассмотрим неоднородно уширенные линии спектральных переходов Γ << kU .  Рассмотрим следующую схему уровней энергии.

 

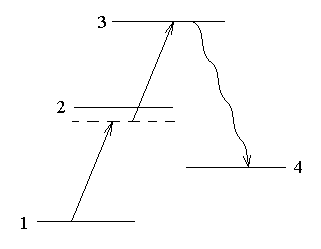
Пусть переходы 1→ 2 и 2 →3 разрешены в дипольном приближении. Как показывает теория, в таком случае переход 1→ 3 обязательно запрещен. То есть

p₁₂ ≠ 0



           p₂₃ ≠ 0.

p13 = 0

Пусть лазерное излучение имеет такую частоту ω, что энергия двух фотонов 2ℏω примерно равна энергии перехода с 1-го уровня на 3-й:

            2ωω⁻ ₃₁ ≈ kU , где k ^{= 2}λ^π — волновое число, U ^{= 2k T}_m^Б       — наиболее вероятная скорость молекул газа.

Пусть уровень энергии 2 находится близко к середине между уровнями 1 и 3, но различие гораздо больше доплеровской ширины линий:

ω31 −ω21>> kU .

2

В эксперименте регистрируется мощность спонтанного излучения на переходе 3→ 4.

          Оптическая схема эксперимента.

 

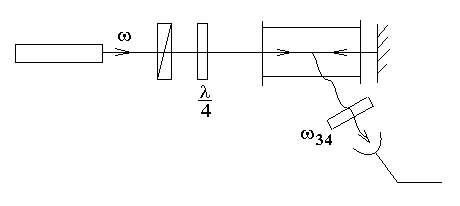
В эксперименте получают следующую зависимость интенсивности на приемнике света от частоты генерации.

 

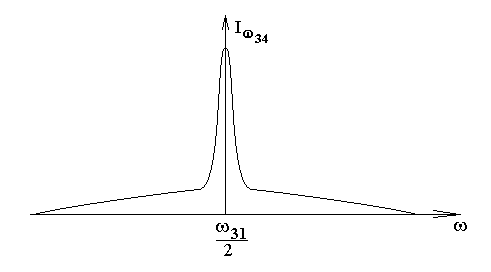
          Качественное объяснение вида зависимости.

Сигнал состоит из двух контуров: узкого высокого и низкого широкого.  Если два фотона поглощаются из встречных световых волн, то в системе отсчета молекулы частоты фотонов будут иметь значения (ω− kV_z ) и (ω+ kV_z ). Тогда из баланса энергии получим:

          ^ℏ(ω− kV_z ) + ^ℏ(ω+ kV_z ) = ℏ^ω₃₁        =>

ω= — узкий по частоте лазера ω сигнал; V_z — любое, то есть в формировании сигнала участвуют молекулы со всеми возможными скоростями, поэтому сигнал имеет большую амплитуду.

Если два фотона поглощаются из одной световой волны, то из баланса энергии в системе отсчета молекулы получим:

          2^ℏ(ω− kV_z ) = ℏ^ω₃₁                            =>

 ω — любое, следовательно, сигнал — широкий контур; V_z = ²ωω−  ³¹ , то

2k есть в формировании сигнала на каждой частоте ω участвует небольшой набор молекул с фиксированной лучевой скоростью, следовательно, сигнал имеет малую амплитуду.

          Количественное описание.

Рассмотрим уравнение Неймана для матрицы плотности ρ:  iℏρ ρ^ɺˆ = ^_Hˆ , ˆ^_,  где Hˆ = Hˆ ₀ ⁻( p E tˆ, ( ⁾) = Hˆ ₀ − pE t^ˆ ( ) — оператор Гамильтона, H^ˆ₀ — невозмущенный световым полем оператор Гамильтона, pˆ — оператор дипольного момента молекулы, E t( ) — напряженность светового поля, pˆ — оператор проекции дипольного момента молекулы на единичный вектор поляризации световой волны.

Пусть для простоты встречные световые волны имеют одинаковую вещественную амплитуду E₀, тогда

         ( )  (    )

                            ω ω1' = − kVz

          Здесь                     

                             ω ω'2 = + kVz

Возьмем уравнение Неймана  iℏρ^ɺˆ = ^_H^ˆ ₀ − pE tˆ ( ),ρ^ˆ_

и раскроем коммутатор  iℏρ ρ ρ^ɺˆ = Hˆ₀ ˆ − ˆHˆ₀ − E t( )⋅( pˆρ ρˆ − ˆ pˆ).

Подставим в это уравнение матрицы операторов в представлении собственных функций невозмущенного оператора Гамильтона Hˆ₀.

           Матрица плотности будет иметь вид произвольной эрмитовской матрицы:

ρ ρ ρ11 12 13   ρ ρ ρ ρˆ =  21 22 23, где ρ ρik = ki* . ρ ρ ρ31 32 33 

Невозмущенный оператор Гамильтона примет в этом представлении диагональный вид:

                            ^E₁       0      0 

         Hˆ₀ = ^ 0   E₂      0 ^.

                           0    0    E3

          Оператор проекции дипольного момента перехода на единичный вектор поляризации       световой     волны, наоборот, имеет          нулевые диагональные элементы:

 0  pˆ =  p21  0 

p12 0 p32

0   p23.  0 

           Здесь учтено, что ^p₁₃ = ^p₃₁ = 0.

Матричные элементы оператора имеют следующий вид:  pnk = ∫ψn* ⋅( p e, )⋅ψk ⋅dV ,

            где p ⁼ ∑q r_{i i} — дипольный момент молекулы, e — единичный вектор

i

поляризации световой волны.

               Выберем фазы собственных функций ^ψ₁ и ^ψ₃ невозмущенного оператора

Гамильтона так, чтобы все матричные элементы проекции дипольного момента

p12 = p21

были вещественными  , тогда p23 = p32

 0  pˆ =  p12  0 

p12 0 p23

0   p23 — оператор проекции дипольного момента на  0 

единичный вектор поляризации световой волны.

Подставим матрицы операторов Hˆ₀,ρˆ, pˆ в уравнение iℏρ ρ ρ^ɺˆ = H^ˆ₀ ˆ − ˆH^ˆ₀ − _{E t}( )⋅( pˆρ ρˆ − ˆ pˆ), перемножим матрицы, добавим феноменологическое затухание и накачку, и получим:

              ρ γρ γρɺ11 + 1                 11 0 −i p E t12ℏ ( )(ρ ρ12 −   21)

                                              = 1   11



                        ρ γρ γρɺ                  +                                 = 0 + i p E t12 ( )(ρ ρ12 − 21) −i p E t23 ( )(ρ ρ23 − 32 )

                 22        2   22       2   22             ℏ                             ℏ



                     ^ρ γρ γρ+                     = + ^{p E t}( )(ρ ρ−         )

               _{                                          ℏ}

                                                                                                                  .

            ρ ωρɺ21 + i 21 21 + Γ12ρ21 = i p E t12 ( )(ρ ρ11 − 22 ) + i p E t23 ( )ρ31

                                                             ℏ                             ℏ

        ρ ωρɺ31 + i 31 31 + Γ13ρ31 = i p E t23ℏ ( )ρ21 −i p E t12ℏ ( )ρ32

           ρɺ32 + ωρ                p E tℏ ( )(ρ ρ22 − 33 ) −i p E t12ℏ ( )ρ31

                                  i 32    32 + Γ23ρ32 = i 23

          Далее нужно выполнить два пункта:

          1). Решить уравнения и найти ^ρ₃₃ .

+∞

            2). Взять интеграл ^Iω34 ~ N 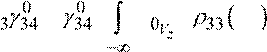 =                              ⋅                                            N       ⋅ ^V_z ⋅^dV_z . Здесь ^γ₃₄⁰ — частота спонтанных переходов с уровня энергии 3 на уровень 4.

Для упрощения решения системы уравнений нужно учитывать принятые приближения: Γ << kU



^_2ωω−≈ kU

                       .

                 ωω− ₂₁>> kU



               ωω− 32>> kU

Чтобы решение не было слишком громоздким, будем считать, что ρ ρ220 = 330 = 0.

Будем искать стационарное решение системы: