Гравитационное поле. Потенциал силы тяжести. Разложение потенциала тяготения в ряд. Сила тяжести на поверхности идеальной Земли. Теорема Клеро

Гравитационное поле

Потенциал силы тяжести

Сила тяжести – равнодействующая силы притяжения Земли и центробежной силы, возникающей вследствие вращения Земли.

1.  Сила притяжения:  По закону Ньютона:

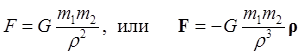
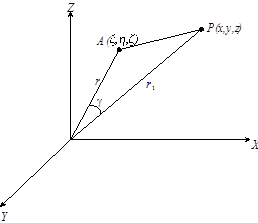
Рассмотрим прямоугольную систему координат с началом в центре масс Земли; ось Z направим по оси вращения, плоскость  xy  совместим с плоскостью экватора (пока – произвольно).

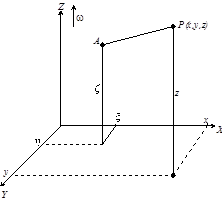
A – точка изучаемого тела

P – точка наблюдения с единичной пробной массой

Сила притяжения точки P телом в проекциях на оси X, Y, Z имеет вид:

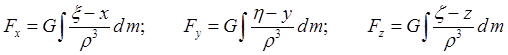
2. Центробежная сила С

Она направлена перпендикулярно к оси вращения:

где r – расстояние до оси вращения.

В проекциях на оси X, Y, Z:

Учитывая, что пробная масса единичная, проекции силы тяжести перепишем как проекции ускорения:

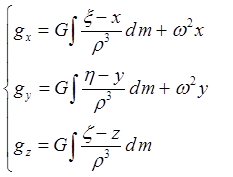
И тогда потенциал силы тяжести имеет вид:

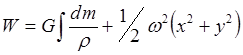
и наоборот: 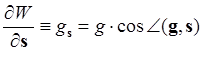– сила тяжести в произвольном направлении s.

В системе XYZ:

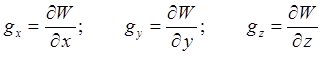
Краткий анализ потенциала:

Свойства:

I.  Потенциал W  внутри Земли (даже в ее центре, т.е. при r ® 0) имеет конечные значения. В частности: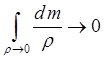

II.  Рассмотрим 2 частных случая:

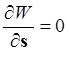1.  Направление s перпендикулярно к g: . Тогда:  и . Это – уравнение поверхности, на которой сила тяжести всюду нормальна к ней. Имеем уровенную поверхность. Одна из таких поверхностей (отвечающая некоторому конкретному значения константы: ), очевидно, совпадает с поверхностью невозмущенной (ветер, приливы) воды Мирового океана. Эту поверхность принимают за фигуру Земли и называют геоидом. Впрочем, сила тяжести на геоиде различна в разных местах (см. теорему Клеро).

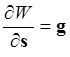2.  Пусть угол . Тогда  и , или 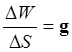. Это означает: если DW – различие потенциалов двух уровенных поверхностей, а DS – расстояние между ними, то это расстояние 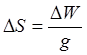 будет разным в разных местах, в обратной зависимости от g.

Разложение потенциала тяготения в ряд

Потенциал силы тяжести:

.

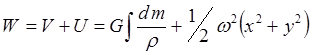Однако, так как ни форма, ни распределение масс «не заданы» для Земли, то выражение «неконструктивно". Разве что для однородного невращающегося шара на его поверхности: .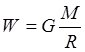

Однако, учитывая факт, что для Земли отклонение от шара невелико, W можно разложить в ряд с небольшим числом “значимых” членов. То же относится и к силе g и, значит, коэффициенты ряда могут быть определены из наблюдений.

Итак, разложим потенциал W в ряд:

Опять: (×) P(x, y, z) – точка наблюдения, (×) A(ξ, η, ζ ) – точка расположения элемента массы dm, r₁ и r – их радиус-векторы, g – угол между r₁ и r.

Тогда: , где  .

Известно разложение:

 

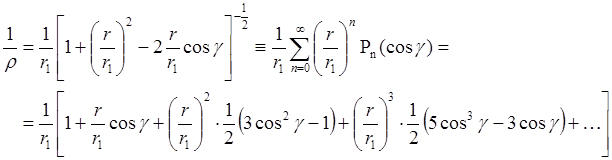
Полиномы Лежандра:

.

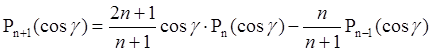Этот ряд сходится при  и расходится при .

Тогда имеем (ограничившись приведенными членами разложения):

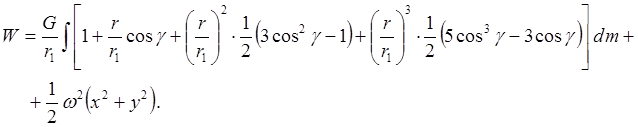
Проанализируем это выражение:

1)  Первый член: 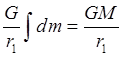 – Потенциал шара.

2)  Второй член:

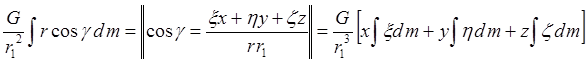
Интегралы в этом выражении – это координаты центра масс тела:

Поместив, по соображениям симметрии, начало координат системы XYZ в этот центр масс, имеем: . Значит, второй член разложения равен нулю:

3)  Третий член (опять подставляем cos g ):

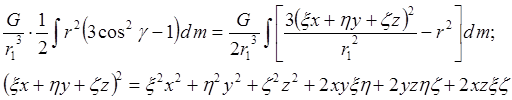         Þ

Интегралы вида:  в механике называются произведениями инерции.

С учетом высокой осевой симметричности Земли можем, направив оси XYZ по главным осям инерции, добиться их равенства нулю.

Третий член станет:

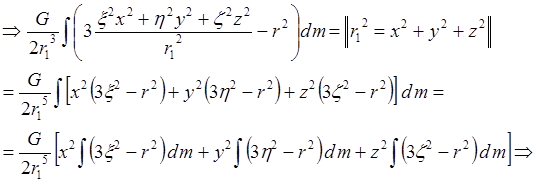
Введем моменты инерции относительно осей X, Y, Z:

, а также, учитывая , получим:

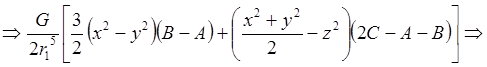
Перейдем к сферическим координатам r, φ, λ (поворот осей X и Y, необходимый для обращения произведений инерции в ноль, изменит только долготу на величину l₀ ):

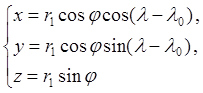
Принимаем l₀ = 0; в итоге, для третьего члена имеем:

 

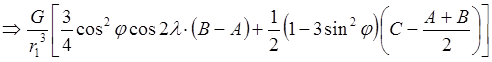
И теперь, собственно потенциал силы тяжести, опустив значок возле r₁ (поскольку по r уже проинтегрировали), запишем: (первый + третий члены):

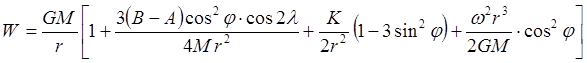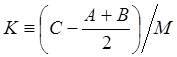, где .  1

Это выражение справедливо до малых второго порядка относительно сжатия a , оно дает уже довольно конкретное (аналитическое) выражение для W.

Приравняв его: W = const – получим уравнения уровеннвх поверхностей. Одна из них (для const = const₀), с точностью до принятых упрощений, отвечает истинной форме Земли, являясь практически геоидом.

Найдем соответствующую const₀, – получим уравнение “дневной” уровенной поверхности. Подставим в 1 координаты одной из точек “реальной” поверхности Земли: φ = 0, λ = 0, r = a. Тогда:

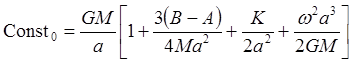          2

Уравнение поверхности примет вид: 1 = 2.

Полученное равенство (ур-ие) можно записать в виде:

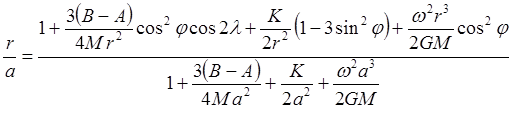
Обозначим:

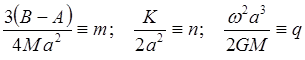
их оценка: .

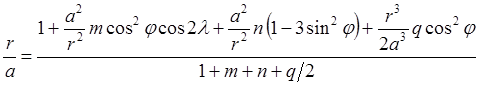
Учитывая порядок величин n, m, q относительно a, принимая  и , заменяя  и отбрасывая q / 2 ~ a, получим:

Так как Земля – тело, близкое к телу вращения, то , поэтому