Опять максимум аномального поля на поверхности: (Vz)max = 4,7 мгл. При осреднении его аномалии с радиусом осреднения R = 2 км получаем: В радиусе R =
2,0 км Þ (Vz)ср = 3,1 мгл Þ и, соответственно: |
В результате аналитического продолжения аномалий на основе экспериментальных данных, относящихся к поверхности измерений, получается распределение аномального поля во всем пространстве, не занятом возмущающими массами.
Опять сравниваем два шара: 1. Шар массой М на глубине z . 2. Шар массой n3М на глубине nz .
Для них имеем: 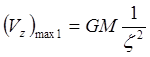 и
и
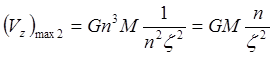 ,
откуда:
,
откуда:![]() .
.
Если в качестве поверхности приведения выбрать плоскость на глубине залегания верхнего тела (H– = z, то есть аналитическое продолжение аномалии в нижнее полупространство), то получим:
![]() и
и 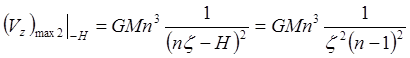 .
.
А поскольку n ¹ 1, то ![]() –
конечная величина и, значит, поле первого шара (Vz)1 при аналитическом продолжении вниз возрастает
быстрее, чем поле второго шара (Vz)2 . Значит, оно подчеркивает
аномалии от неглубоких тел, по сравнению с глубокими. Если же, напротив,
аномалии (Vz)1 и (Vz)2 продолжить вверх на высоту H+ = z, то:
–
конечная величина и, значит, поле первого шара (Vz)1 при аналитическом продолжении вниз возрастает
быстрее, чем поле второго шара (Vz)2 . Значит, оно подчеркивает
аномалии от неглубоких тел, по сравнению с глубокими. Если же, напротив,
аномалии (Vz)1 и (Vz)2 продолжить вверх на высоту H+ = z, то:
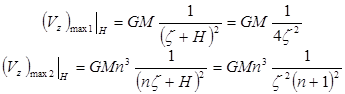 ,откуда:
,откуда:
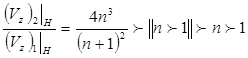 .
.
Учитывая, что на первоначальной поверхности оно было равно n, а здесь, на высоте Н, оно оказалось большим (> n), видим, что аналитическое продолжение вверх подчеркивает региональная составляющая по сравнению с локальной.
Вспомним сведения из теории преобразований Фурье: Пусть F(x) – практически любая непериодическая функция, Тогда:
![]() ,
где
,
где 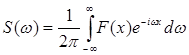 ;
;
здесь w – пространственная частота; ее размерность: [w] = рад/м; S(w) – комплексный спектр функции F(x).
Теорема сложения:
Если ![]() ,
то
,
то ![]() .
.
Теорема смещения: Пусть![]() ,
тогда
,
тогда ![]() .
.
Док-во: 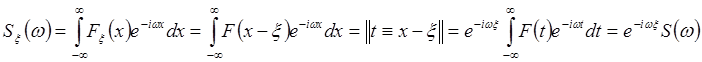 .
.
Спектр производной:
Если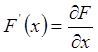 ,
то
,
то ![]() .
.
Доказательство: 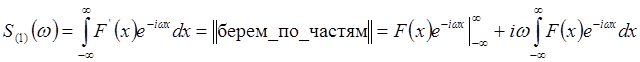 .
.
![]() Но
Но ![]()
![]()
![]() поскольку
поскольку
![]()
![]() ,
сл-но:
,
сл-но:![]()
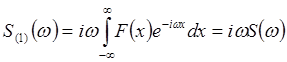 .
Аналогично:
.
Аналогично:![]()
![]()
![]() Для производной по параметру:
Для производной по параметру:![]()
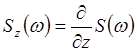 .
.
![]()
![]() Случай
двухмерных аномалий (горизонтальный цилиндр):
Случай
двухмерных аномалий (горизонтальный цилиндр):
![]()
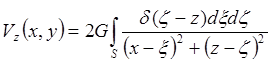 .
.![]() Спектр:
Спектр: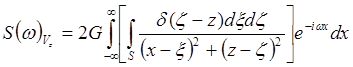 .
.
Меняем порядок
интегрирования: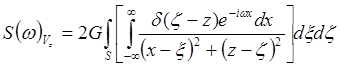 .
.
Учтем, что для интеграла в квадратных скобках имеет место:
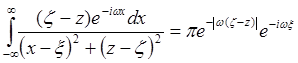 .Опуская
знак модуля при w в экспоненте (для
удобства), имеем:
.Опуская
знак модуля при w в экспоненте (для
удобства), имеем:
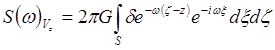 .
(a) Принимая
для плоскости наблюдений z = 0, получаем:
.
(a) Принимая
для плоскости наблюдений z = 0, получаем: 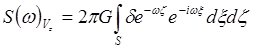 .
А так как производная по параметру:
.
А так как производная по параметру: 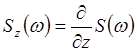 ,
–то можем из (a) получить:
,
–то можем из (a) получить: 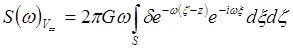 .
Сравнив его с (a) , имеем:
.
Сравнив его с (a) , имеем: ![]() и
вообще:
и
вообще:![]() .
Для пл-ти наблюдений z = 0:
.
Для пл-ти наблюдений z = 0: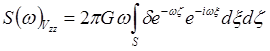 .
Учитывая теорему Пуассона, для магнитного поля получим:
.
Учитывая теорему Пуассона, для магнитного поля получим: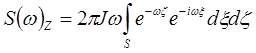 .
Для горизонтальных составляющих:
.
Для горизонтальных составляющих: 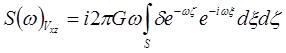 и:
и:
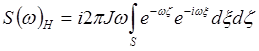 .
.
|
|
Рассмотрим принципы аналитического продолжения – на примере продолжения в верхнее полупространство. Пусть ось Z направлена вверх, Q1 и Q2 – две бесконечные плоскости , перпендикулярные оси Z. На одной из них (на плоскости Q1) зададим некую функцию U(x,y,z). Ни сама плоскость Q1 , ни все пространство вверх от нее не должны содержать особых точек. |
Для двухмерных возмущающих тел можно записать (на плоскости Q1 – для прямой Q1(x’,z’)):
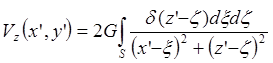 ,
а для прямой Q2(x”,z”) на плоскости Q2 :
,
а для прямой Q2(x”,z”) на плоскости Q2 :
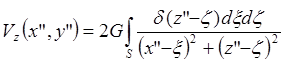 .Их
спектры, соответственно (так же, как и при выводе формулы (a)):
.Их
спектры, соответственно (так же, как и при выводе формулы (a)):
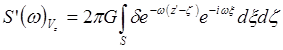 ,
,
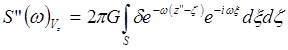 .
.
Поделив их одно на
другое, получаем:![]() .
.
Здесь ![]() –
частотная характеристика аналитического продолжения
–
частотная характеристика аналитического продолжения ![]() с
уровня z’ на
ур-нь z”.
с
уровня z’ на
ур-нь z”.
Можно и наоборот: ![]() –
с характеристикой аналитического продолжения:
–
с характеристикой аналитического продолжения: ![]()
Окончательное
выражение: 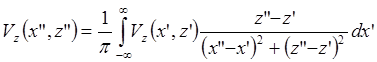 .
.
Это – интеграл Пуассона для перехода (пересчета поля) на верхний уровень.
Покажем на примере производных Vxz и Vzz, что интеграл Пуассона справедлив и вообще для любых производных поля.
|
По теоремам: |
|
|
О спектре производной: |
О спектре производной по параметру: |
|
|
|
|
и тогда, умножив (b) на iw или w, получим: |
|
|
·iw: |
·w: |
Аналогично тому, как выведено выражение для Vz(x”,z”), имеем:
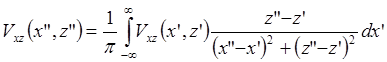 .
.
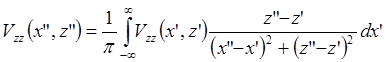 .
.
Для магнитного поля – по теореме Пуассона получаем:
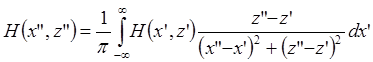 .
.
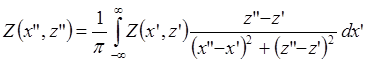 .
.
В рамках спектрального анализа решается и задача выражения одних производных потенциала через другие: VxÛVz.
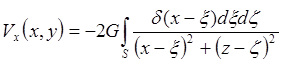 .
.![]() Спектр:
Спектр: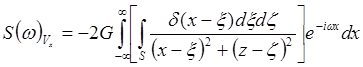 .
.
(Изменяем порядок
интегр-ния, заменяем: x – x = t,). Спектр становится: ![]() .
.
Вспомним также: ![]() .Сравнивая
их, видим:
.Сравнивая
их, видим:![]() .
.
Записав это выражение
для плоскостей Q1 и Q2 на нашем рисунке, т.е. для спектров S’(w) и S”(w)
соответствующих функций, получим, аналогично прежнему случаю: (для Vz имели: ![]() ):
):
![]() .Отсюда
опять получаем формулу:
.Отсюда
опять получаем формулу:
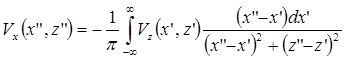 .Полагая
плоскости Q1 и Q2 совпадающими (z” = z’), получим для одной
.Полагая
плоскости Q1 и Q2 совпадающими (z” = z’), получим для одной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.