Горизонтальная материальная полоса (горизонтальная материальная плоскость, горизонтальный тонкий пласт)

Сделаем краткий обзор решения прямой задачи для ряда других простых тел:

4. Горизонтальная материальная полоса (горизонтальная материальная плоскость, горизонтальный тонкий пласт)

Пусть на глубине Н (наше прежнее z)имеется горизонтальная полоса шириной 2l с поверхностной плотностью m. Начало координат расположим над серединой полосы и обозначим через q угол, под которым видна полоса из точки наблюдения. Тогда получим:

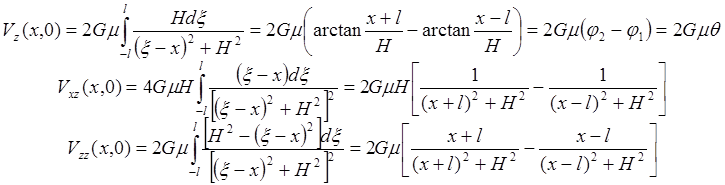
Представления о подобной полосе могут быть применены при определении аномальных полей от:

1)  горизонтальных пластовых рудных залежей небольшой мощности;

2)  прочих пологих плоских удлиненных структур с углами падения 1–3 градуса.

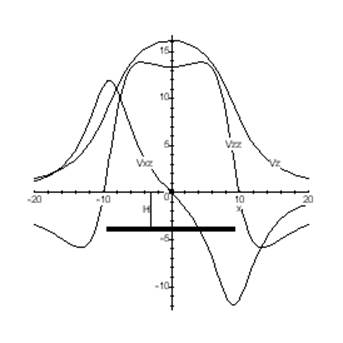
Найдем абсциссы х_1/2 и х_1/4 точек, где значения V_z равны, соответственно, (V_z)_max/2 и (V_z)_max/4 (нетрудно показать, что (V_z)_max = 4Gmarctan(l/H).Они равны:

и; и тогда:

5. Горизонтальная полуплоскость

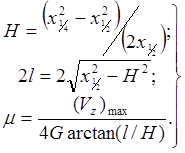
Поместив начало координат над границей полуплоскости, получим (опять m – поверхностная плотность):

  

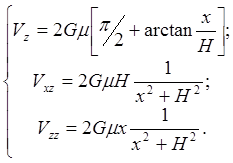
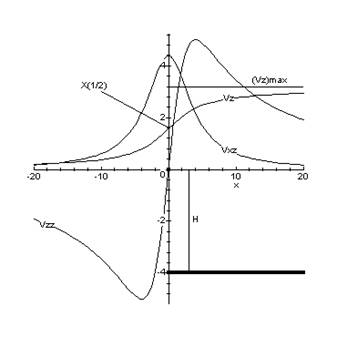
Характеристические точки кривых:

1. Для V_xz:   х_1/2 = Н;

2. Для V_zz:   имеет экстремумы в точках х = ± Н.

3. Максимум V_xz  «отбивает» край полуплоскости.

4. (V_z )_max = 2Gpm.

Из более сложных – объемных объектов– рассмотрим

6. Вертикальный контакт (вертикальная ступень, вертикальный уступ)

Под вертикальной ступенью в теории интерпретации аномалий понимается горизонтальный полупласт бесконечного простирания по оси у, ограниченный вертикальной гранью, отличающийся по плотности (намагниченности) от вмещающей среды. – График и его характеристики подобны графику для горизонтальной полуплоскости.

Характеристические точки: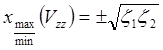 , где z₁ и z₂ – глубины верхней и нижней границ контакта.

Принципы решения прямой задачи для тел произвольной формы

Все способы решения прямой задачи для тел произвольной формы основаны на замене – разбиении возмущающего тела суммой тел простейшей формы. Так действие куполов, брахиантиклиналий, брахисинклиналий (брахи = короткий) с крутыми склонами иногда подобно действию шара; действие вытянутых антиклиналей и синклиналей с крутыми склонами – подобно действию горизонтального кругового цилиндра; тонкие пласты – плоскостям; тектонические нарушения – наклонным и вертикальным ступеням; вертикальные жилы и дайки – вертикальным материальным полосам (линиям) и т.п.

1. Вычисление эффекта (аномалии) при помощи аналитического продолжения

Рассмотрим ситуацию:

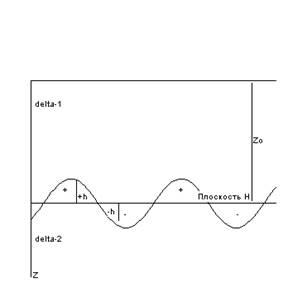
Пусть для плотностей имеет мести: d₂ > d₁. Если отклонения h ( или Dh) от плоскости Н невелики, по сравнению с горизонтальными размерами тела, то разбиваем каждую «волну» на цилиндрики, для которых на плоскости Н имеет место:

.

Зная V_z на плоскости Н, можем аналитически продолжить его на плоскость приведения.

2. Способ эквивалентной замены

Иногда возмущающее тело можно «аппроксимировать» эквивалентным телом, лежащим вне контактной поверхности (см. рисунок). Решение будет тем точнее, чем ближе рельеф антиклинали подобен полю V_z от шара.

3. Вычисление аномалии путем разбиения тела на вертикальные столбики

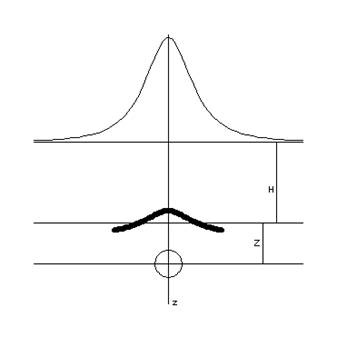
Пусть разбиение на столбики выполнено по системе кольцевых секторов: поместив начало координат в точку, для которой вычисляется гравитационный эффект (x = y = z = 0), а также исходя из системы:, имеем:

rk    ji                                         ji+1 rk+1                      h2   h2

, где  и     . Суммируя по всем окружающим нашу точку элементам, имеем: , мгл (i  и k см. из рисунка)

Связь между магнитными составляющими Z_a, H_a и DT.

Косое намагничивание объектов

Практика магниторазведки пока кщк (и особенно в случае аэромагнитной съемки) такова, что компонентная съемка не реализуется, измеряется же так называемое «приращение» модуля полного вектора индукции (напряженности) геомагнитного поля по отношению к некоторой «начальной» точке:             (a).

С другой стороны, до сих пор мы при решении прямой задачи для магниторазведки постоянно повторяли тезис об обязательном вертикальном намагничивании изучаемых тел и, соответственно, теорему Пуассона мы использовали в варианте вертикального намагничивания «простейших» тел. Однако чисто вертикальное намагничивание в природе необязательно и вообще нечасто – хотя бы потому, что и вертикальное поле на Земле имеет место лишь возле магнитных полюсов. И все же «преимущества» теоретического подхода в рамках вертикального намагничивания оюъектов настолько существенны, что при интерпретации аномалий используются-таки именно «вертикальные» подходы (формулы).

I. Выведем формулы перехода от составляющих  Z_a и H_a к DT

Пусть векторТ₀ расположен в плоскости 0xz, тогда:

      ;

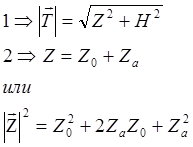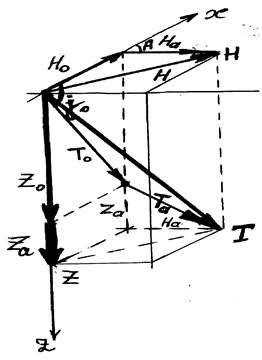
аналогично (учтем, что сами Z₀ и H₀  выражаются через Т₀ ):

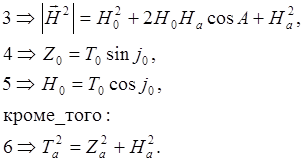
Подставляя все это в формулу (a), получим (DT – это уже только величина, скаляр):

.

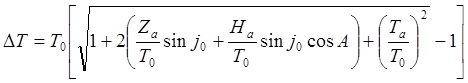Учитывая малость подкоренных слагаемых: 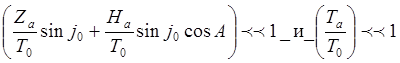, разлагаем правую часть в ряд. В итоге:

Это выражение верно при DT до тысяч гамм.

II. Определение аномального поля (Z_a и H_a) при произвольном направлении намагничивания тел

Пусть Z_a и H_a  – аномальные элементы для случая вертикальной намагниченности тел, а  Z’_a  и  H’_a   – ‘элементы аномального поля при косом намагничивании