Настоящее пособие содержит материал 12 лекций специального курса "Термодинамикагетерогенного зародышеобразования", читаемогона кафедре статистической физики СПбГУ для магистрантов физического факультета. Эти лекции объединены тем, что в них рассматриваются общие закономерности нуклеации на растворимых макроскопических ядрах различных типов, какснизкой, таки свысокой растворимостью, как поверхностно-инактивных, такиповерхностно-активных.
Пособие опирается на цикл оригинальных работ авторов и включает многоновыхрезультатов, ранее опубликованных тольков журнальном видеи поэтому мало доступных для студентов. Пособие позволяет студентам контролировать понимание изучаемого в курсе лекций материала и может быть полезным для всех специалистов по вопросам фазовых превращений первого рода.
ББК 31.211
© ,
Ф. М. Куни, 2002
© С.-Петербургский государственный университет, 2002
Данное пособие посвящено выводу основных термодинамических соотношений теории нуклеации паров на присутствующих в этих парах посторонних частицах, растворимых в конденсирующейся из пара влаге. Инициирующая роль гетерогенных центров в фазовых превращениях первогорода уже давно привлекает внимание исследователей. То, чтонекоторыетакиецентры способны резкоснижать порог устойчивости метастабильного состояния фазы и вызывать интенсивное фазовое превращение, является ответственным за многие природные явления и находит широкое применение в различных технологиях. Характерным и наиболее распространенным в атмосфере Земли примером инициирующих гетерогенных центров конденсациипаров воды какраз иявляются частицы, растворимые в зарождающихся на них из пара каплях. Как правило, эти частицы имеют макроскопический размер (10−6 ÷10−4 см) иприрастворениив водеобразуют молекулярный или ионный раствор. Будет ли растворение ядра в каплях полным или не полным, зависит от размера ядра и растворимости его вещества. Если вещество ядра является поверхностно-активным, то процесс растворения ядра вкаплесопровождается формированием адсорбционного монослоя поверхностно-активного вещества (ПАВ) на поверхности капли и образованием молекулярных агрегатов (мицелл) в объеме капли. Установление в явном виде связей между параметрами и характерными особенностями различных растворимых ядер, с одной стороны, и интенсивностью процесса зарождения капель, с другой, и будет нашейзадачей.
Рассмотрим каплю, которая находится в паре и представляет собойраствор вещества ядра в конденсате (жидкости, конденсирующейся из пара). В качестве переменной описания капли выберем число молекул ν конденсата в капле. Общеечисломолекул растворенного в каплевещества ядра (илиобщеечислоионов этоговещества, если оно является электролитом и при растворении диссоциирует) обозначим через νn . Будем пока предполагать, что вещество ядра конденсации является поверхностно-инактивным и адсорбцией растворенного веществаядранаповерхностизарождающейсякаплиможнопренебречь.
Как убедимся далее, при полном растворении макроскопического ядра конденсации в капле во всей важной для термодинамики нуклеацииобластипеременной ν соблюдаетсянеравенство
ν
νn
>>1. (1.1)
При
выполнении этого неравенства раствор в капле будет разбавленным по отношению к
веществу ядра: относительная концентрация x раствора равна
малой величине ν
νn.
При этом поверхностное натяжениекаплии удельный молекулярный объем конденсата
можно считатьтакимиже, какивотсутствиерастворенноговещества.
Обозначим через bν зависящийот переменной описания капли ν химический потенциал конденсата в капле. Выражаем bν в единицах k TB , где kB – постоянная Больцмана и T – температура, и отсчитываем от значения, соответствующего равновесию чистого конденсата с паром при плоской поверхности их соприкосновения. Химический потенциал конденсата, играющего роль растворителя для вещества ядра, определяется вкладами от капиллярного и осмотического давлений в капле, но от пересыщения пара практически не зависит, так как капля является плотным по сравнению с паром образованием. Вклад от капиллярного давления дается известным соотношением Гиббса– Кельвина (таким же, как для химического потенциала конденсата в гомогенной капле), а вклад от осмотического давления в случае разбавленного раствора находится по формуле Вант-Гоффа. Записываяэтивкладывпеременной ν , находим
bν
=
c2 3haν−13 −
ν νn , (1.2) где
a =
c4πγk TB
hc3 4vα πh23 , (1.3)
γ
– поверхностноенатяжениекапли из чистого конденсата, vα
– молекулярный объем конденсата (здесь и в дальнейшем индексами α
и β
будем отмечать величины, относящиеся соответственно к жидкой и газовой
фазам). Величину a в дальнейшем будем называть
безразмернымповерхностнымнатяжениемконденсата.
Вчастности, из (1.2) видим, чтопри ν = ν0 , где
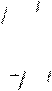ν0 =
c9 2νn ah32 , (1.4)
достигаетсямаксимум bν какфункции ν
, равный
c hbν max = 4a 9ν130 . (1.5)
Дажеприотносительномалыхзначениях ν , прикоторых раствор в капле может быть не разбавленным, а соотношение (1.2) может не соблюдаться, химический потенциал должен все же монотонно убывать с уменьшением ν вследствие термодинамической устойчивости раствора. Поэтому найденный максимум у bν единствен в области полногорастворенияядравкапле.
Обозначим через b химический потенциал пара. Как и bν , выражаем b вединицах k TB иотсчитываем от значения, соответствующего равновесию пара с конденсирующейся жидкостью при плоской поверхности их соприкосновения. При равновесии капли и пара должно соблюдаться равенство b b= ν . Согласно (1.2) и (1.5) это равенство может иметь место только при b < c hbν max . При 0 < <b c hbν max уравнение b b= ν имеетдвакорня
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
