Полосы равной толщины и в интерферометре Майкельсона. Интерферометр Жамена. Интерферометр Рождественского (Маха-Цендера)

подынтегральных слагаемых отличаются только косинусами.

Подставим сюда k = ¹ ⋅ ²π= ¹ и получим окончательное выражение 4π π λ λ4   2

ikr

                             E_P = −                           E₀ r ⋅   ⋅(_cos(^α₀) + _cos( )^α )⋅dS .                                                      (4)

S

Эта формула представляет поле в точке наблюдения P, как сумму полей вторичных источников света, расположенных на поверхности S замкнутой вокруг точки наблюдения P.

---------

Проанализируем амплитуду излучения каждого вторичного источника света в точке наблюдения P.

Амплитуда пропорциональна площади излучающей площадки dS , комплексной амплитуде поля E₀(r) в точке вторичного источника и обратно1

пропорциональна ~  расстоянию r от вторичного источника до точки

r

1

наблюдения P. Зависимость амплитуды от расстояния вида ~        хорошо r

согласуется с тем фактом, что через любую сферу проходит одинаковая энергия, тогда интенсивность спадает с расстоянием обратно-пропорционально

1

площади сферы ~                   , а амплитуда ведет себя, как корень из интенсивности

2

r

      1                                                                                                          ^ikr

~  . Амплитуда в точке P имеет фазовый множитель e , который r

определяется запаздыванием фазы kr в точке наблюдения относительно фазы вторичного        источника. Кроме         того, амплитуда вторичного           источника пропорциональна сомножителю

           , который называют коэффициентом наклона. Коэффициент наклона описывает зависимость излучательной способности вторичного источника света от направления волны пришедшей ко вторичному источнику и волны ушедшей от вторичного источника.

Экзамен. Применение теории Кирхгофа к дифракции света на отверстии произвольной формы в плоском экране.

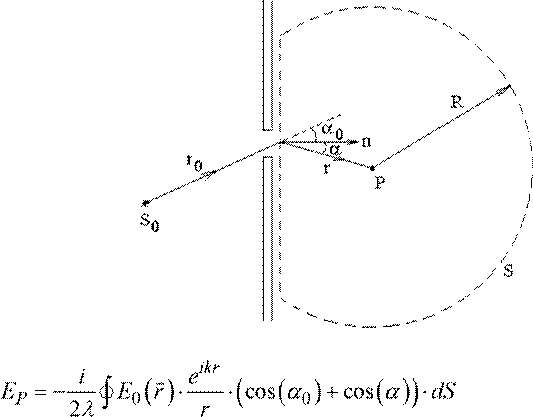
S

В качестве охватывающей точку наблюдения P поверхности S выберем сферу с радиусом R и центром в точке P. Часть сферы, которая находится до экрана, с другой стороны экрана от точки наблюдения, заменим плоскостью, расположенной вплотную к экрану со стороны точки наблюдения P.

           Мысленно разобьем поверхность S на три части:

           S = S₁ + S₂ + S₃, где

          S₁ — поверхность оставшейся справа от экрана части сферы,         S₂ — плоская поверхность, примыкающая непосредственно к экрану,      S₃ — поверхность отверстия в экране.

Согласно Кирхгофу интеграл нужно брать только по поверхности S₃, так как оба других интеграла стремятся к нулю, по крайней мере, при стремлении радиуса сферы R к бесконечности.

      ∫ →0, так как световое поле за непрозрачным экраном очень мало.

S₂

          Факультативная вставка.

Сложнее показать, что ∫ →0. Это происходит только благодаря R→∞

S₁

сомножителю в виде коэффициента наклона. И действительно, с одной стороны, на большом расстоянии R от отверстия амплитуда E₀ поля

1

вторичных источников на поверхности сферы спадает с расстоянием E₀ ~                                                                                                         , и

R

                                     eikr                                                                                                       1

сомножитель      в подынтегральном выражении спадает, как ~ , так как r         R

r R= , но с другой стороны, площадь поверхности сферы растет S ~ R². Поэтому, казалось бы, интеграл должен стремиться к константе. Этого не происходит из-за коэффициента наклона. Для вторичных источников на поверхности сферы α^≡ (n,−r) ^{= −}( n r, ) = 0_{, где} (−_n) — внешняя нормаль к сфере, и, следовательно, cos(α) =1.

      cos(^α₀) = cos(n r, ₀) = −cos(−n r, ₀), где угол (−n r, ₀) очень мал при больших значениях R.

          Тогда

^

  cos(α₀) = −cos(−n r, ₀) = −cos(πα− ₀) ≈ −_1₋ (^πα−₂ ⁰)^{2 }__                                                                                                            =>



         cos( )α + cos(α0) ≈ −1 1− (πα−2 0)2  = (πα−2 0)2 .

          При больших значениях R угол (πα⁻ ₀) — мал: πα⁻ _{0 ~} ¹ . Тогда R

cos( )α + cos(^α₀) ~ ¹₂ . R

  Учитывая, что E₀ ~ R1 , S ~ _R², cos( )α + cos(^α₀) ~ R¹₂ , получим

        ∫ ~ 12 ⋅ R2 ⋅ 12 ~ 12 →R→∞ 0.

                  S₁ R             R       R

В результате интегралы по поверхностям S₁ и S₂ малы, и ими можно пренебречь.

          Конец факультативной вставки.

          По теории Кирхгофа для дифракции на отверстии в плоском экране достаточно         суммировать         излучение   вторичных источников           только         по поверхности отверстия по формуле

ikr

                             EP = − E0 r ⋅   ⋅(cos(α0) + cos( )α )⋅dS .

Здесь E r — комплексная амплитуда светового поля в плоскости отверстия,  r —вектор из точки наблюдения P в точку вторичных источников на поверхности отверстия,

^α₀ —угол между лучом, пришедшим к отверстию, и нормалью к экрану n,

α — угол между нормалью к экрану n и направлением (−r) от вторичного