каким знаком входят в определитель 6-го порядка произведения:
а) a23a31a42a56a14a65; б) 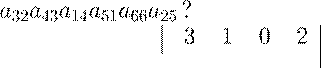
Задача. Вычислить определитель 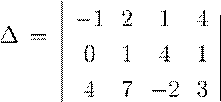 .
.
Решение. Упростим определитель, пользуясь его свойствами: из
4-ой строки вычтем 1-ую:
¯
 .
.
Поясним сделанные преобразования: (1) - к 1-ой строке прибавили 2-ую строку, умноженную на 3; (2) - к 4-ой строке добавили 2-ую.
Теперь разложим определитель по 1-ому столбцу:
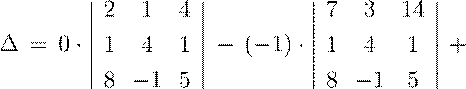
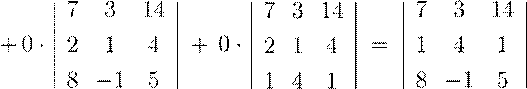 .
.
Из 3-его столбца вычтем удвоенный 1-ый столбец, затем разложим по 3-ему столбцу
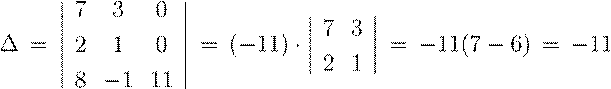 .
.
29. Исходя только из определения детерминанта, доказать, что определитель матрицы
α1 α2 α3 α4 α5
β1 β2 β3 β4 β5
a1 a2 0 0 0
b1 b2 0 0 0 c1 c2 0 0 0
равен нулю.
30. Разложить по элементам 1-го столбца и вычислить определитель матрицы a 1 1 1
b 0 1 1
.
c 1 0 1 d 1 1 0
31. Пользуясь формулой Крамера, вычислить A−1, если:
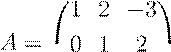 .
.
0 0 1
32. Найти ранг матрицы:
0 4 10 1
10 18 40 174 8 18 7 .
1 7 17 3
Задача. Решить систему[3]
 .
.
Решение. Вычитаем из 2-ой строки утроенную 1-ую, из 3-ей утроенную 1-ую, из 4-ой – 1-ую. Получим
¯
1 1 2 3 ¯¯ 1
0 −4 −5 −11 ¯¯ −7
¯ .
0 1 −5 −7 ¯¯ −8
0 1 1 −4 ¯ −5
Вторую строку умножим на (-1) и переставим 2-ую и 4-ую строки (это делается для удобства счета). Дальнейшие переходы обозначены стрелками:
1 1 2 3 ¯¯ 1 1 1 2 3 ¯¯ 1
¯ ¯
→ 0 10 1 −15 −−47 ¯¯¯¯ −5 → 0 10 1 −16 −−34 ¯¯¯¯ −−53 →
−8
¯ ¯
0 4 5 11 7 0 0 1 27 27
1 1 2 3 ¯¯ 1
¯
0 1 1 −4 ¯¯ −5 →
0 0 1 27 ¯¯ 27
¯
0 0 2¯ 1 1 1 1 2 3 ¯¯ 1
1 1 2 3 ¯¯ 1 ¯
0 1 1 −4 ¯¯ −5 0 1 1 −4 ¯¯ −5 .
→ ¯ → 0 0 1 27 ¯¯ 27
0 0 1 27 ¯¯ 27 ¯
0 0 0 −58 ¯ −58 0 0 0 1 1
Прямой ход выполнен, система оказалась совместной. Так как ранг левой части равен числу неизвестных, то решение единственно (это случай крамеровой системы).
Теперь совершаем обратный ход: из 3-ей строки вычитаем 4-ую, умноженную на 27, к 2-ой строке прибавим 4-ую, умноженную на 4, из 1-ой вычитаем 4-ую, умноженную на 3:
1 1 2 3 ¯¯ 1 1 1 2 0
¯
→ 0 1 1 −274 ¯¯¯¯ −275 → 0 1 1 00 0 1 0
0 0 1
¯
0 0 0 1 1 0 0 0 1
1 1 0 0 ¯¯ −2 1 0 0 0
¯
→ 0 1 0 00 0 1 0 ¯¯¯¯ −1 → 0 1 0 00 0 1 0
0
¯
0 0 0 1 1 0 0 0 1
Ответ: x1 = −1, x2 = −1, x3 = 0, x4 = 1.
33. Решить систему:
x1 − 2x2 + x3 + x4 = 1,
x1 − 2x2 + x3 − x4 = −1, x1 − 2x2 + x3 + 5x4 = 5.
Задача. Вычислить обратную для матрицы[4]
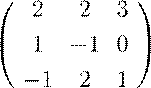 .
.
Решение.
¯ ¯ 2 2 3 ¯ 1 0 0 1 −1 0 ¯
¯ ¯ 1 −1 0 ¯¯ 0 1 0 → 2 2 3 ¯¯
¯ ¯
−1 2 1 0 0 1 −1 2 1
¯ ¯ 1 −1 0 ¯ 0 1 0 1 −1 0 ¯
¯ ¯ → 0 4 3 ¯¯ 1 −2 0 → 0 1 1 ¯¯
¯ ¯ 0 1 1 0 1 1 0 0 −1
¯ ¯ 1 0 0 ¯ 1 −4 −3 1 0 0 ¯
¯ ¯
→ 0 1 0 ¯¯ 1 −5 −3 → 0 1 0 ¯¯
¯ ¯ 0 0 −1 1 −6 −4 0 0 1
![]()
¯ −2
¯
¯
¯ −1 →
¯
¯ 0
¯
¯
1
¯ −1
¯
¯
¯ −1 .
¯
¯ 0
¯
¯
1
0 1 0
1 0 0 →
0 0 1
0 1 0
0 1 1 →
1 −6 −4
1 −4 −3 1 −5 −3 .
−1 6 4
Ответ: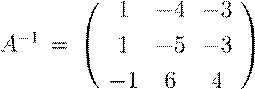 .
.
34. Вычислить обратную матрицу для данной матрицы A:
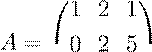 .
.
1 0 1
35.
Являются ли векторы (1,2,0),
(0,1,0), (−1,0,2) линейно
зависимыми?
§2.1. Программа коллоквиума во 2 семестре.
Линейные пространства (вещественные и комплексные), определение, аксиоматика и простейшие следствия, примеры линейных пространств. Линейная зависимость и независимость, примеры. Шесть теорем о линейной зависимости и независимости. Базис в линейном пространстве, теорема о единственности разложения по базису. Размеренность пространства: теорема "подготовительная"и теорема о базисности набора из n линейно-независимых векторов в n-мерном пространстве. Примеры базисов. Изоморфизм линейных пространств. Сохранение линейной зависимости (независимости) при изоморфизме. Критерий изоморфности конечномерных линейных пространств. Примеры. Подпространства (п/п). Сумма и пересечение подпространств. Прямая сумма п/п. Единственность разложения в прямую сумму. Формула для размерности суммы п/п (без доказательства). Примеры. Подпространство решений однородной линейной системы уравнений. Его размерность. Базис и фундаментальная система решений. Общее решение. Неоднородная линейная система (НЛС). Общее решение НЛС.
Линейные операторы в линейных пространствах. Примеры. Матрица оператора. Пространство операторов и базис в нем, размерность. Композиция операторов и матрица композиции. Собственные значения и собственные векторы матриц. Линейная независимость собственных векторов для матриц с простым спектром. Характеристический полином матрицы и вычисление его некоторых коэффициентов. Алгебраическая и геометрическая кратности. Теорема о соотношении алгебраической и геометрической кратностей (с доказательством). Подобные матрицы. Инварианты подобия. О приведении матрицы к диагональному виду подобным преобразованием (Основная теорема). Преобразование координат вектора и матрицы оператора при замене базиса. Функции от матриц. Два способа определения. Тождество Кэли (без доказательства).
Билинейные формы. Квадратичные формы. Приведение квадратичной формы к сумме квадратов. Метод Лагранжа и другие методы. Закон инерции квадратичной формы. Индексы инерции.
Ядро и образ оператора. Теорема Фредгольма о разрешимости линейного уравнения.
Евклидовы пространства. Аксиомы скалярного произведения в вещественном евклидовом пространстве. Неравенство Коши-Буняковского-Шварца и неравенство треугольника. Примеры. Лемма < Ax,y >Rn= < x,Aty >Rn. Комплексные евклидовы пространства. Неравенство Коши-Буняковского-Шварца и неравенство треугольника. Примеры. Лемма < Ax,y >Cn=< x,A∗y >Cn. Ортогональность и линейная независимость. Теорема Пифагора. Угол между векторами. Ортонормированая система. Примеры. Ортогонализация системы векторов по Шмидту.
Коллоквиум (начало апреля).
Задачи 1-9 соответствуют материалу коллоквиума, остальные – материалу экзамена во втором семестре.
2.1.1. Линейные пространства.
Задача. Решить однородную систему 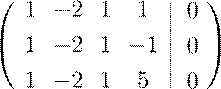 .
.
Решение. В результате последовательных преобразований получаем
¯
1 −2 1 1 ¯ 0 µ ¯ ¶
¯
0 0 0 −2 ¯¯¯ 0 → 10 −02 1 10 1 ¯¯¯ 00 →
0 0 0 4 0
µ ¯ ¶
→ 1 −2 1 00 1 ¯¯¯ 00 .
0 0
Ранг матрицы левой части равен двум, следовательно, можно выразить два неизвестных через остальные. Выберем в качестве базисного минора, например, минор, образованный 1-м и 4-м столбцами, тогда 1-е и 4-е неизвестные определятся единственным образом через 2-е и 3-е. Значения 2-го и 3-го неизвестного остаются произвольными, эти неизвестные называются свободными, а 1-е и 4-е главными.
Ответ: x1 = 2x2 − x3 , x4 = 0, векторы-столбцы (−1,0,1,0)t, (2,1,0,0)t образуют базис в пространстве решений.
Задача. Решить систему
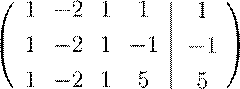 .
.
Решение. Система отличается от предыдущей наличием правых частей. Совершая аналогичные преобразования, получаем равносильную систему
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.