Матрицы и определители. Действия над матрицами. Умножение матриц. Квадратные матрицы. След матрицы

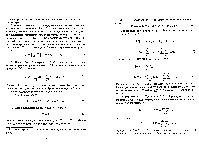
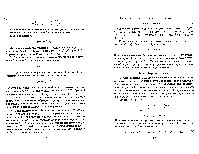
любом случае число беспорядков изменится на единицу, и четность перестановки поменяется. Рассмотрим теперь общий случай. Пусть переставлены местами и 7++8+1, s > О. Эту транспозицию можно осуществить так. Переставим ik последовательно с 'lk=1, П +2, . . „1, на что потребуется ( s + 1) ”соседних” транспозиций. Затем последовательно переставим с . . . , п +1, что потребует

23

еще з ”соседних” транспозиций. Таким образом, четность изменится 2.9 + 1 раз, т.е. окажется противоположной исходной.

Легко понять, что любую перестановку 1 можно перевести в любую другую перестановку З некоторым числом транспозиций. Этот результат может быть достигнут различными способами. Однако, если четность 1 и одинакова, то число транспозиций обязательно четно, ибо каждая транспозиция меняет четность. Напротив, если четность Т и различна, то число потребных транспозиций нечетное. В частности, любая четная перестановка получается из тождественной четным, а нечетная перестановка — нечетным числом транспозиций.

Всего различных перестановок порядка п имеется п!. КоЛИЧеСТВО четных и нечетных перестановок одинаково и равно п! /2. Эго следует из того, что ес.ум мы все п! перестановок одновременно подвергнем какой-нибудь одной и той же транспозиции, то четные перестановки перейдут в нечетные и наоборот.

Перестановкам сопоставляют знак перестановки Е(Т): Е(Т) = +1, если Т — четная; Е(Т) = —1, если Т — нечетная.

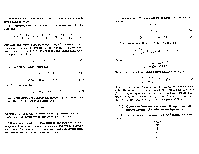
2. Подстановки. Подстановкой порядка п называется взаимно однозначное отображение множества, состоящего из п, различных предметов, на себя. Пронумеруем эти предметы. Пусть первый предмет отображается в предмет с номером Й , второй — в предмет с номером и т.д. Числа 1 = (i1 , образуют перестановку, которая однозначнр определяет нашу подстановку. Символически это можно записать так:

                                                         — (1,1),                       (1)

22, где о рассматриваемая подстановка. Ту же подстановку можно записать и иначе. Пусть в первый предмет переходит предмет с номером Л, во второй — с номером 92, и т.д. Тогда

 запишется в виде

(2)

1, 2,

Например,

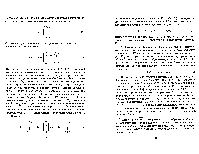
1.2 з,5

Вообще, ясно, что можно записать в виде

(з) ь,

если (З) получено из (1) применением одной и той же перестановки к элементам обеих строк формулы (1). Таким образом, подстановка с определяется парой перестановок (К, С), определенных с точностью до одной и той же перестановки над элементами К и С. Вместо (1)—(3) удобно коротко писать с = (1,1) = (3, 1) (К, С).

Тождественную подстановку будем обозначать через 1, :

где — любая перестановка.

Совокупность всех подстановок обозначим через 'Рп. Так как всякая подстановка единственным образом записывается в виде (1), то множество РП содержит п! элементов.

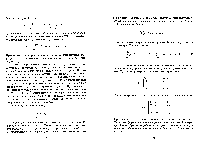
З. Произведение подстановок. Выполняя последовательно подстановки (отображения) т и о, мы снова получим подстановку, отвечающую композиции ЭТиХ отображений. Эта подстановка обозначается через от и называется произвеДением подстановок т и о. Это произведение при п > 2 не коммутативно: от и тс, вообще говоря, различны. При образовании произведения от удобно представить т и о в виде т = о (К, С). Ясно, что тогда ст = (1, С). Например, пусть

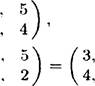1. 2. з,

з. 5, 2, 1, 4

                                   1, 2.  4,                              З, 5. 2, 1. 4

5, З. 4, 1. 2

25

Тогда

Упражнение. Найдите для этого примера подстановку тоПриведем свойства произвеДения поДстановок.

1.  Ассоциативность:

џ(от) = (щт)т.

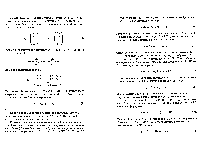
Для доказательства представим подстановки в виде: т

(I,k),                         (ЮС), = (С, 3). Тогда ст = (1, С), џ(ст) =

С другой стороны, џо (К, 3), (џс)т = (I, З). о

2.  Существование ”единицы". Для тождественной подстановки и любой подстановки с, очевидно,

10 = от- = с.

З. Существование обратной подстановки. Для любой подстановки ст существует подстановка р, такая что

ро = ор 1.

Подстановка р называется обратной к подстановке о и обозначается через б—1 . Легко понять, что для о = (1, 1) обратной является подстановка -1 = (1. I). В частности, 1

Свойства 1, 2, З означают, что множество подстановок РП с операцией произведения образует группу, то есть множество с ассоциативной внутренней операцией, в котором существует единица и каждый элемент имеет обратный.

4. Знак подстановки. Знаком подстановки о = (К, С) называется ЧИСЛО Е ( б)  Проверим корректность этого определения. Знак Е(с) зависит только от о, но не от того, какой именно парой перестановок задается с. В самом деле, если элементы К и С подвергнуть одной и той же перестановке, то четность и К, и С либо сохранится (если выполняемая перестановка четная), либо изменится. В обоих случаях произведение останется прежним.

26

Очевидно, Е(1) = 1. Покажем теперь, что

                                                                         (4)

Для доказательства представим подстановки в виде