Математика \ Линейная алгебра и аналитическая геометрия

Билинейная форма. Определение, примеры. Пространство билинейных форм. Оператор билинейной формы. Изображающая матрица билинейной формы, страница 3

12. 


Пусть — подпространство вещественного евклидова пространства Е. Пусть О х е Е и х = у + z, где у Е- Е, 'z Е FL . Доказать, что из всех векторов подпространства F наименьший угол с х образует вектор у, причем равенство cos(x,y) = cos(x, где у] Е- Е, выполняется тогда и только тогда, когда у] = ау с некоторым а > О.

13.  Пусть Оп — вещественное евклидово пространство полиномов степени S п (с вещественными коэффициентами) на отрезке [—1, 1]. Скалярное произведение полиномов P(t) и Q(t) задано формулой (Р, Q) = f_11 P(t)Q(t) dt. Проверьте, что полиномы Лежандра, заданные формулами

P0(t) = 1, Pk(t) = 1   — 1) k], К = 1 2kk!

образуют ортогональный базис пространства оп. Докажите, что при ортогонализащш системы 1, t, е, .... , tn получится базис, отличающийся от ПОлиНОМОВ Лежандра лишь множителями.

14.  В R4 найти угол между подпространствами F и G, где F = C{et, е2}, G =

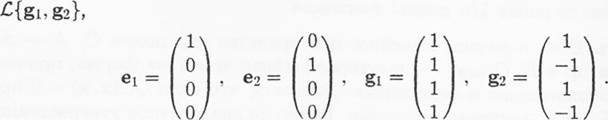
з


15.  В комплексном евклидовом пространстве мп (п х п)-матриц (с комплексными элементами) со скалярным произведением (с, у) = Тт доказать следующие свойства: а) всякая унитарная матрица имеет норму, равную УЛ; Ь) линейный оператор А в мп , заданный умножением на унитарную матрицу и: Ас = их,  е Мп , является унитарным оператором.

16.  В комплексном евклидовом пространстве Мп (п х п)-матриц (с комплексными элементами) со скалярным произведением (с, у) Trcy* задан оператор А умножения на матрицу а € мп : Ах = ас, т; е мп , и оператор В умножения на эрмитово сопряженную матрицу Ь = Г: вс Ьс, т. е мп . Доказать, что

17.  Пусть Б — вещественное евклидово пространство тригонометрических полиномов степени п (т. е., функций вида

                       f(t) = ао + cost + Ь1 sint + ап cos nt + Ьп sin nt

с вещественными коэффициентами). Скалярное произведение задано формулой

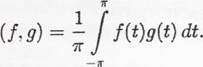
Проверить, что оператор

dt2

симметричен в Е и доказать, что система функций

1

cos t, sin t, , cosnt, sin nt

образует ортонормированный собственный базис для оператора А.

18.  В вещественном евклидовом пространстве полиномов степени п, заданных на отрезке [—1, 1], со скалярным произведением

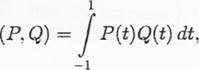
рассматривается оператор А, заданный соотношением

                                                     (АР)@) = (t2 —                 + 2tP(t).

Проверьте, что А * = А.

19.  Пусть А — самосопряженный неотрицательный оператор в комплексном евклидовом пространстве Е. Доказать, что существует такой самосопряженный

4

неотрицательный оператор В, что выполнено В 2 А. Доказать, что В положителен, если А положителен.

20.  Пусть А и В — самосопряженные неотрицательные операторы в комплексном евклидовом пространстве Е, причем оператор В обратим. Доказать, что собственные значения оператора АВ неотрицательны.

21.  Пусть ненулевые векторы х и у в комплексном евклидовом пространстве Е имеют одинаковую норму: Их П — Иу Л. Доказать, что существует унитарный оператор С в Е, переводящий х в у: Сх = у.

22.  Пусть А — самосопряженный оператор в комплексном евклидовом пространстве Е. Доказать следуюпдие свойства:

а) оператор А — iI обратим;

Ь) оператор D (А — И) -1 (А + iI) унитарен;

с) оператор В — обратим;

          d) выполнено тождество А          —           + 1).

23.  Пусть А и В — самосопряженные операторы в комплексном евклидовом пространстве Е, причем оператор А положителен. Доказать, что собственные значения оператора АВ вещественны.

24.  Пусть А — самосопряженный оператор в комплексном евклидовом пространСтве Е. Доказать, что следующие свойства эквивалентны:

а) А) € [а, З] для всех собственных значений А) оператора А,

Ь) оператор А — AI отрицателен при А > З и положителен при А а.

25.  Пусть А и В — самосопряженные положительные операторы в комплексном евклидовом пространстве Д и выполнено А ВС, где С — унитарный оператор. Доказать, что С = 1.

26.  Доказать, что в разложении А = ВС для линейного оператора А в комплексном евклидовом пространстве Е, где В — самосопряженный неотрицательный оператор и С — унитарный оператор (полярное разложение), оператор В определен однозначно.

27.  Для линейного оператора А в комплексном евклидовом пространстве Е доказать, что оператор А * А неотрицателен. При этом А*А положителен тогда и только тогда, когда А обратим.

5

Скачать файл