З. В (п 2) рассматривается квадратичная форма
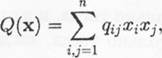(lij = qji € R.
Доказать, что для положительной определенности этой формы
условие qjj О, 
1 . . , п,
является необходимым, но не достаточным. 
4. Пусть Ё — п-мерное линейное пространство над полем R, и Q(x, у) — СиМметричная билинейная форма с индексами инерции = п, п_ = О. Доказать, что имеет место неравенство
Q(x + у, х + у) S Q(x, х) + Q(Y' У)' Ух, у Е- Е, причеМ равенство имеет место для тех и только тех векторов х, у, для которых выполнено ах = Ду при некоторых неотрицательных числах а, р, одновременно не равных нулю.
5.
Найти индексы инерции квадратичной формы Q(c) Тт с2 в
линейном пространстве Мп , образованном (п х п)-матрицами с
вещественными элементами.
6. Доказать, что ортогональная проекция ребра п—мерного куба (в Р) на его диагональ равна 1/n длины диагонали.
7. Пусть Е — п-мерное линейное пространство над полем С, А — линейный оператор в Е, Q(x, у) — полуторалинейная эрмитова форма, причем Q(x, х) — положительно определенная. Доказать, что если Q(Ax, х) О при любом х Е, то А — нулевой оператор. Верно ли аналогичное утверждение, если Е
2
— п-мерное линейное пространство над полем и Q(x, у) — симметричная
билинейная форма с индексами = п, п— = О ?
б. Пусть Е = мп —
комплексное евклидово пространство (п х п)-матриц (с комплексными элементами)
со скалярным произведением (а, Ь) = Тт ab*. Пусть F {а € мп : Tra =
0} — подпространство матриц с нулевым следом. Найти ортогональное дополнение 
О. Пусть D = — вещественное евклидово
пространство (п х п)-матриц (с вещественными элементами) со скалярным
произведением (а, Ь) = Тт аЫ. Пусть F — подпространство симметричных матриц.
Найти ортогональное дополнение FL
10. Пусть fl, . . . — ортонормированная система векторов в Р. Доказать, что для любого х € справедливо неравенство Бесселя
Е(х , lxlI2.
Неравенство обращается в равенство (равенство Парсеваля)
для любого х Е RB тогда и только тогда, когда К = п, т. е. система 
образует
ортонормированный базис в Р.
11. Пусть х, у € Р, х О, у 74 О. Доказать, что а) х = ау, где а 0, тогда и только тогда, когда угол между х и у равен нулю.
б) х ау, где а < О, тогда и только тогда, когда утол между х и у равен т.
12.
 |
|||
 |
|||
13. Пусть Оп — вещественное евклидово пространство полиномов степени S п (с вещественными коэффициентами) на отрезке [—1, 1]. Скалярное произведение полиномов P(t) и Q(t) задано формулой (Р, Q) = f_11 P(t)Q(t)dt. Проверьте, что полиномы Лежандра, заданные формулами
P0(t) = 1, Pk(t) = 1 
К = 1, . . 
2kk! dtk образуют ортогональный базис пространства оп. Докажите, что при ортогонаЛИЗащш системы 1, t, е, .... , Р получится базис, отличающийся от полиномов Лежандра лишь множителями.
14. В R4 найти угол между подпространствами F и G, где F = C{et, е2}, G =
з
— п-мерное линейное пространство над полем и Q(x, у) — симметричная
билинейная форма с индексами = п, п— = О ?
б. Пусть Е = мп —
комплексное евклидово пространство (п х п)-матриц (с комплексными элементами)
со скалярным произведением (а, Ь) = Тт ab*. Пусть 
{а € мп :
Tra = 0} — подпространство матриц с нулевым следом. Найти ортогональное
дополнение р ш .
0. Пусть D = мп — вещественное евклидово пространство (п х п)-матриц (с вещественными элементами) со скалярным произведением (а, Ь) = Тт аЫ. Пусть F — подпространство симметричных матриц. Найти ортогональное дополнение FL
10. Пусть fl, — ортонормированная система векторов в р. Доказать, что для любого х € справедливо неравенство Бесселя
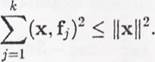
Неравенство обращается в равенство (равенство Парсеваля)
для любого х Е RB тогда и только тогда, когда К = п, т. е. система 
образует
ортонормированный базис в Р.
11. Пусть х, у € Р, х О, у О. Доказать, что а) х = ау, где а 0, тогда и только тогда, когда угол между х и у равен нулю.
б) х ау, где а О, тогда и только тогда, когда утол между х и у равен т.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.