ортогональным преобразованием подобия к диагональному виду.
5. Привести унитарным преобразованием подобия к диагональному виду самосопряженную матрицу
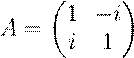 , где i — мнимая единицу, т.е. i2 = −1.
, где i — мнимая единицу, т.е. i2 = −1.
6. Привести унитарным преобразованием подобия к диагональному виду ортогональную матрицу
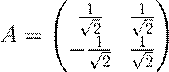 .
.
Квадратичные формы. Кривые и поверхности второго порядка
1.Выразить квадратичную форму
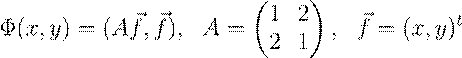 ,
,
через координаты вектора f~. Решение.
µ ¶ µ ¶ µ ¶
Af~ = 1 2 · x = x + 2y ,
2 1 y 2x + y
(Af,~ f~) = (x + 2y)x + (2x + y)y = x2 + 4xy + y2.
2. Найти симметричную 3 × 3-матрицу A, отвечающую квадратичной форме Φ(x,y,z) = x2 − 3xy + yz:
Φ(x,y,z) = x2 − 3xy + yz = (Af,~ f~), f~ = (x,y,z)t. Решение. Для симметричной матрицы
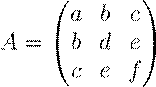 ,
,
и вектора f~ = (x,y,z)t справедливо равенство
(Af,~ f~) = ax2 + dy2 + fz2 + 2bxy + 2cxz + 2eyz.
Сравнивая последнее выражение с
исходной квадратичной формой Φ(x,y,z)
= x2 − 3xy + yz, получим: ![]()
![]() ,
т.е.
,
т.е.
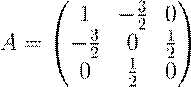 .
.
3. Привести квадратичную форму
Φ(x,y,z) = x2 + 2xy + 2y2 + 4xz + 5z2
к сумме квадратов методом Лагранжа (выделением полных квадратов). Определить какого типа поверхность задает уравнение Φ(x,y,z) = 1.
Решение. Выделим полный квадрат из слагаемых содержащих переменную x:
Φ = (x + y + 2z)2 + y2 + z2 − 4yz.
Сделаем замену переменных:
 ,
,
и получим Φ = x21+y12+z12−4y1z1. Выделив в последнем выражении полный квадрат, прийдем к равенству
![]() .
.
Сделав замену переменной
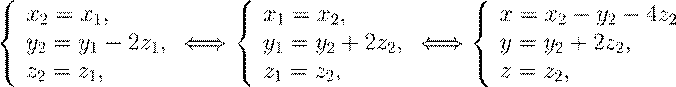 ,
,
окончательно получим Φ = x22 + y22 − 3z22. Уравнение Φ(x,y,z) = 1 ⇐⇒ x22 + y22 − 3z22 = 1 задает однополстной гиперболоид. Отметим, что метод Лагранжа не дает возможности определить полуоси гиперболоида. Разные замены переменных могут привести к уравнению α1x˜2 + α2y˜2 + α3z˜2 = 1, и коэффициенты α1, α2 и α3 зависят от используемой замены переменных. При этом, согласно закону инерции квадратичных форм, число положительных, отрицательных и нулевых чисел среди α1, α2 и α3 не зависит от замены переменных, что и позволяет определить тип поверхности.
4. Привести квадратичную форму
Φ(x,y,z) = 2x2 + y2 − 4xy − 4yz
к сумме квадратов при помощи ортогонального преобразования. Определить какого типа поверхность задает уравнение Φ(x,y,z) = 1 и найти метрические характеристики этой поверхности.
Решение. Квадратичная форма Φ(x,y,z) = 2x2 + y2 − 4xy − 4yz может быть записана в виде
Φ(x,y,z) = (Af,~ f~), где
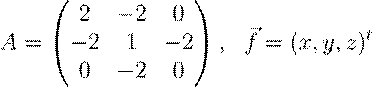 .
.
Приведем матрицу A ортогональным преобразованием подобия к диагональному виду. Это заведомо возможно, т.к. матрица симметрична. Характеристический многочлен матрицы A имеет вид
¯
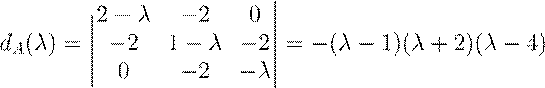 .
.
Можно найти нормированные собственные векторы![]() ,
,
![]() ,
отвечающие собственным значениям
,
отвечающие собственным значениям
λ1 = 1, λ2 = −2, λ3 = 4. Векторы ![]() автоматически
оказываются ортогональными друг другу и образуют ортонормированный базис в R3.
автоматически
оказываются ортогональными друг другу и образуют ортонормированный базис в R3.
Составим теперь ортогональную матрицу T из столбцов![]() :
:
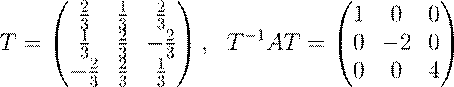 .
.
Делая в квадратичной форме Φ(x,y,z) = 2x2+y2−4xy−4yz замену переменных
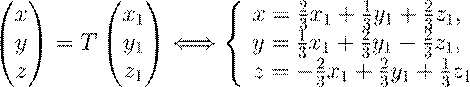 ,
,
получим Φ = λ1x21
+ λ2y12 + λ3z12
= x21 − 2y12 +
4z12. Уравнение Φ(x,y,z) = 1 ⇐⇒ x21 − 2y12
+ 4z12 = 1 задает однополостной
гиперболоид с полуосями ![]() (вещественными)
и
(вещественными)
и ![]() (мнимой).
(мнимой).
5. Методом Лагранжа преобразовать уравнение x1x2 + x1 + x2 = 1 к стандартному виду и определить тип кривой. Решение. Сделав следующее преобразование координат
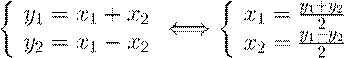
получим уравнение ![]() .
Выделяя в этом уравнении полный квадрат:
.
Выделяя в этом уравнении полный квадрат:
![]() ,
,
и делая новую замену переменных:
 ,
,
получаем
![]() .
.
Таким образом, уравнение задает гиперболу. Определить ее полуоси методом Лагранжа невозможно.
6. Ортогональным преобразованием и сдвигом преобразовать уравнение x2 + y2 + z2 − 2xy − 2zx − 2yz + 2x = 1 к стандартному виду, определить тип поверхности и ее метрические характеристики. Решение. Прежде всего приведем квадратичную форму Φ(x,y,z) = x2 + y2 + z2 − 2xy − 2zx − 2yz к каноническому виду ортогональным преобразованием. Квадратичная форма Φ(x,y,z) может быть записана в виде
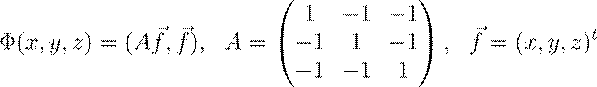 .
.
Диагонализуем симметричную матрицу A ортогональным подобным преобразованием. Характеристический многочлен матрицы A имеет вид dA(λ) = −(λ − 2)2(λ + 1). Решая задачу (A − 2I)~x = ~0, получим общее решение ~x = C1(−1,1,0)t +
C2(−1,0,1), ортогонализуя и нормируя полученную фундаментальную систему решений, получаем два ортогональных и нормированных собственных вектора, отвечающих собственному значению
![]() .
.
Третий нормированный собственный
вектор, ортогональный двум пред√ыдущи√м,
соо√тветствует
собственному значению![]()
(1/ 3,1/ 3,1/ 3)t.
Далее, составим ортогональную матрицу T
из столбцов![]() :
:
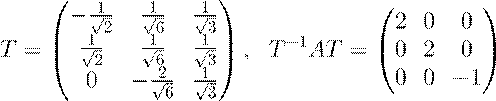 .
.
При замене переменных
 ,
,
уравнение переходит в следующее: ![]()
1. Выделим в последнем уравнении полные квадраты:
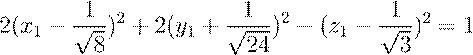 .
.
Сделав замену переменной
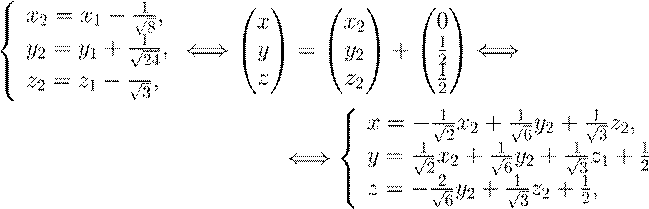 ,
,
приходим к уравнению 2x22
+ 2y22 − z22 =
1 однополостного гиперболоида с полуосями ![]() (последняя
полуось — мнимая). Задачи для самостоятельного решения 1. Выразить квадратичную
форму
(последняя
полуось — мнимая). Задачи для самостоятельного решения 1. Выразить квадратичную
форму
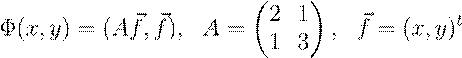 ,
,
через координаты вектора f~.
2. Найти симметричную 3 × 3-матрицу A, отвечающую квадратичной форме
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.