











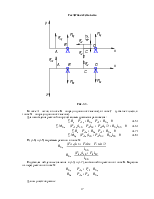









нахождения реакций опор составляем уравнения равновесия:
![]() (4.5)
(4.5)
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
![]() (4.8)
(4.8)
Из (4.6) и (4.8) выражаем реакции в точке D:
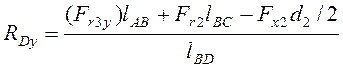
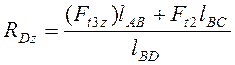
Подставляя найденные значения в (4.5) и (4.7), можно найти реакции в точке В. Выразим их через реакции в точке D:
![]()
![]()
Длины участков равны:
Lab=84мм
Lbc=57мм
Lbd=145мм
Подставляем численные значения в выражения для реакций:
Rdy=(5526·0.084+2872·0.057)/0.145=4330Н
Rdz=(15180·0.084+7590·0.057)/0.145=11780Н
RBy= -5526+2872-4330=-6984Н
RBz=-15180+7590-11780=-19370Н
Построим эпюры моментов. Для этого определим моменты в точках В и С:
MBz=(Fr3y)Lab=5526·0.084=464.2Н×м
MCzп=(Rdy)Lcd=4330·0.089=385.37Н×м
MCzл=(Fr3y)Lac+RByLbc=375.552Н×м
MBy=(Ft3z)Lab=15180·0.084=1275Н×м
MCy=(RDz)Lcd=11780·0.089=1048Н×м
Здесь ![]() и
и ![]() - изгибающий момент соответственно
в правой и левой частях точки С.
- изгибающий момент соответственно
в правой и левой частях точки С.
Для построения эпюры суммарного момента вычислим суммарный изгибающий момент в точках В и С:
![]() Н×м
Н×м
![]() Н×м
Н×м
![]() Н×м
Н×м
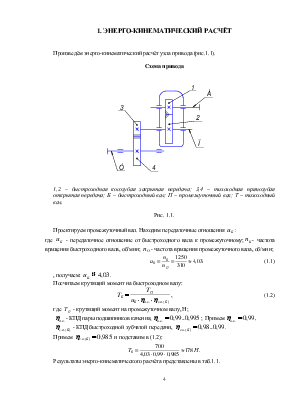
Эпюры изгибающих и крутящего моментов показаны на рис.3.4 -3.7.
Эпюра изгибающего момента Mz
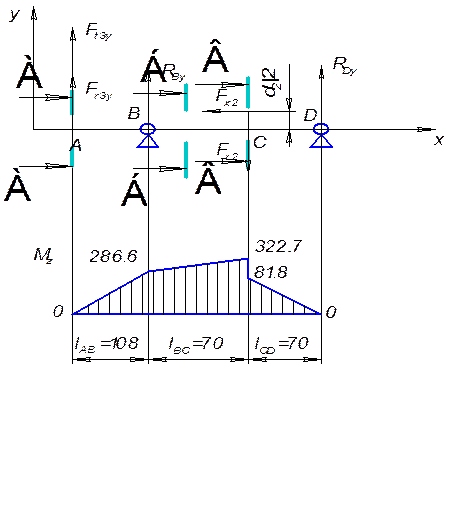
Рис. 3.4.
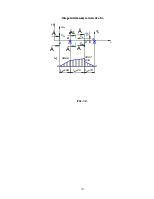
Эпюра изгибающего момента My
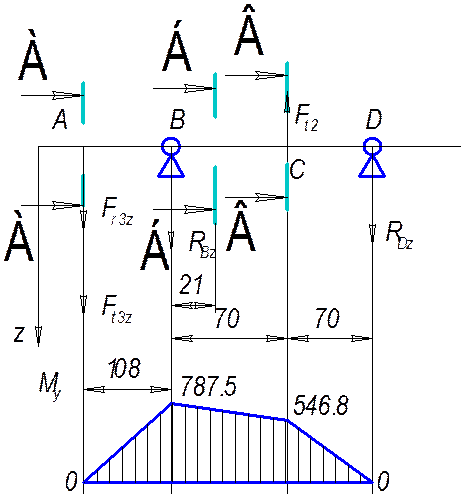
Рис. 3.5.
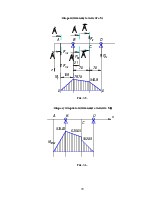
Эпюра суммарного изгибающего момента MS
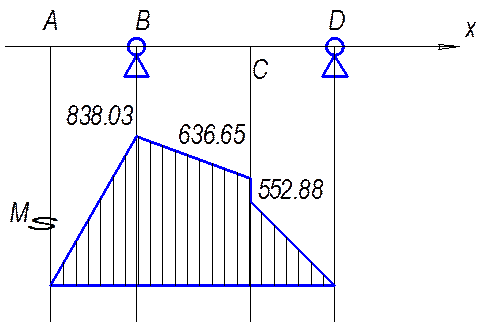
Рис. 3.6.
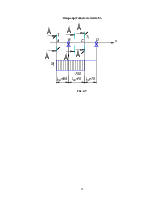
Эпюра крутящего момента Mx
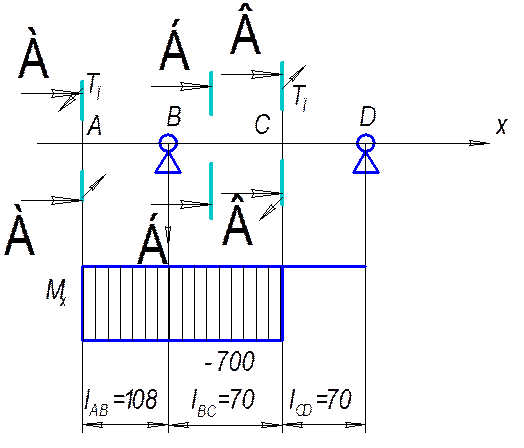
Рис. 4.7.
3.3. Проверочный расчёт вала
Уточнённый проверочный расчёт вала заключается в определении коэффициентов запаса (3.9) в опасных сечениях и проверки условия (3.10) [1].
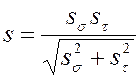 , (3.9)
, (3.9)
где ![]() -
коэффициент запаса прочности по нормальным напряжениям, вычисляется по формуле
(3.11);
-
коэффициент запаса прочности по нормальным напряжениям, вычисляется по формуле
(3.11); ![]() - коэффициент запаса прочности по
касательным напряжениям, вычисляется по формуле (3.12).
- коэффициент запаса прочности по
касательным напряжениям, вычисляется по формуле (3.12).
![]() ,
(3.10)
,
(3.10)
где ![]() -
допускаемый коэффициент запаса прочности.
-
допускаемый коэффициент запаса прочности.
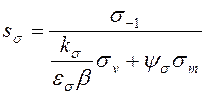 ,
(3.11)
,
(3.11)
где ![]() -
предел выносливости стали при симметричном цикле изгиба, для углеродистых
конструкционных сталей вычисляется по формуле (3.13);
-
предел выносливости стали при симметричном цикле изгиба, для углеродистых
конструкционных сталей вычисляется по формуле (3.13); ![]() -
эффективный коэффициент концентрации нормальных напряжений;
-
эффективный коэффициент концентрации нормальных напряжений; ![]() - масштабный фактор для нормальных
напряжений;
- масштабный фактор для нормальных
напряжений; ![]() - коэффициент влияния
шероховатости поверхности, принимаем его равным 0,95;
- коэффициент влияния
шероховатости поверхности, принимаем его равным 0,95; ![]() -
амплитуда цикла нормальных напряжений, равная наибольшему напряжению изгиба
-
амплитуда цикла нормальных напряжений, равная наибольшему напряжению изгиба ![]() в рассматриваемом сечении;
в рассматриваемом сечении; ![]() - среднее напряжение цикла
нормальных напряжений, в нашем случае рана нулю,т.к. осевая нагрузка равна нулю;
- среднее напряжение цикла
нормальных напряжений, в нашем случае рана нулю,т.к. осевая нагрузка равна нулю;
![]() - коэффициент чувствительности к
асимметрии цикла для нормальных напряжений, принимаем его равным 0,2.
- коэффициент чувствительности к
асимметрии цикла для нормальных напряжений, принимаем его равным 0,2.
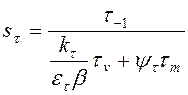 ,
(3.12)
,
(3.12)
где ![]() -
предел выносливости стали при симметричном цикле кручения, для конструкционных
сталей вычисляют по формуле (3.14);
-
предел выносливости стали при симметричном цикле кручения, для конструкционных
сталей вычисляют по формуле (3.14); ![]() - эффективный
коэффициент концентрации касательных напряжений;
- эффективный
коэффициент концентрации касательных напряжений; ![]() -
масштабный фактор для касательных напряжений;
-
масштабный фактор для касательных напряжений; ![]() -
амплитуда цикла касательных напряжений, равная наибольшему напряжению изгиба
-
амплитуда цикла касательных напряжений, равная наибольшему напряжению изгиба ![]() в рассматриваемом сечении;
в рассматриваемом сечении; ![]() - среднее напряжение цикла
касательных напряжений;
- среднее напряжение цикла
касательных напряжений; ![]() - коэффициент
чувствительности к асимметрии цикла для касательных напряжений, принимаем
равным 0,1.
- коэффициент
чувствительности к асимметрии цикла для касательных напряжений, принимаем
равным 0,1.
![]() ,
(3.13)
,
(3.13)
где ![]() -
предел выносливости, для стали 40X он равен 650 МПа.
-
предел выносливости, для стали 40X он равен 650 МПа.
Т.о., предел выносливости равен
![]() МПа
МПа
![]() МПа (3.14)
МПа (3.14)
Значения ![]() и
и
![]() определяют в предположении, что
вследствие колебания крутящего момента
определяют в предположении, что
вследствие колебания крутящего момента ![]() напряжения
кручения изменяются по отнулевому циклу (315).
напряжения
кручения изменяются по отнулевому циклу (315).
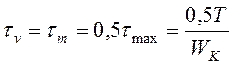 ,
(3.15)
,
(3.15)
где ![]() -
максимальное напряжение цикла;
-
максимальное напряжение цикла; ![]() - момент
сопротивления сечения кручению.
- момент
сопротивления сечения кручению.
Производим расчёт по сечению Б – Б. Выписываем коэффициенты ![]() и
и
![]() для вала с галтелью(d=48мм,
D=63мм,
для вала с галтелью(d=48мм,
D=63мм, ![]() мм),
мм), ![]() и
и ![]() :
:
![]()
![]()
![]()
![]()
Ищем ![]() :
:
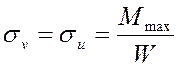 ,
,
где ![]() -
максимальный изгибающий момент в сечении Б – Б, Н∙м;
-
максимальный изгибающий момент в сечении Б – Б, Н∙м; ![]() -
момент сопротивления сечения вала изгибу, м3.
-
момент сопротивления сечения вала изгибу, м3.
Вычисляем момент сопротивления:
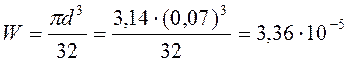 м3
м3
Максимальный изгибающий момент в сечении Б – Б находим по формуле (4.17).
![]() (4.17)
(4.17)
Изгибающие моменты ![]() и
и
![]() находим по эпюрам:
находим по эпюрам:
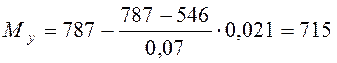 Н×м
Н×м
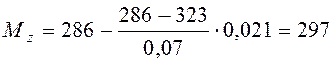 Н×м
Н×м
Подставляем найденные значения изгибающих моментов в (4.17):
![]() Н×м
Н×м
Таким образом,
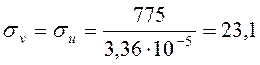 МПа
МПа
Найдём момент сопротивления сечения вала кручению:
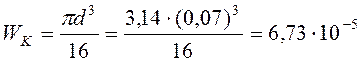 м3
м3
По формуле (3.15)
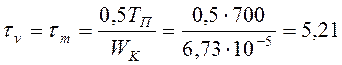 МПа
МПа
По формуле (3.13)
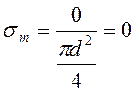
Подставляем полученные значения в (3.11) и (3.12):
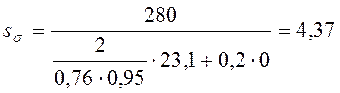
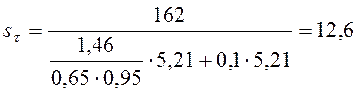
Вычисляем коэффициент запаса прочности (3.9):
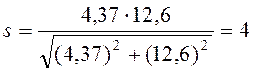
Вывод: условие прочности (3.10) в сечении Б – Б выполняется:
![]()
Рассмотрим сечение В – В. В этом сечении концентратором напряжений является шпоночная канавка. Выписываем необходимые коэффициенты (диаметр вала d=60мм):
![]()
![]()
![]()
![]()
Ищем ![]() :
:
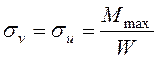
Момент сопротивления сечения изгибу вычисляется по формуле:
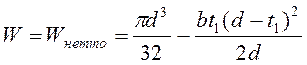 ,
,
где ![]() -
ширина шпонки, м;
-
ширина шпонки, м; ![]() - глубина посадки шпонки
на валу, м;
- глубина посадки шпонки
на валу, м; ![]() - диаметр вала в м.
- диаметр вала в м.
Таким образом,
м3
По эпюрам находим изгибающие моменты ![]() и
и ![]() :
:
![]() Н×м
Н×м
![]() Н×м
Н×м
Подставляем найденные значения изгибающих моментов в (4.17):
![]() Н×м
Н×м
Таким образом,
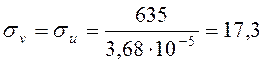 МПа
МПа
Момент сопротивления сечения вала кручению определяется следующим образом:
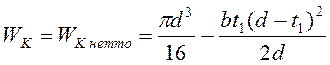
Подставляем численные значения:
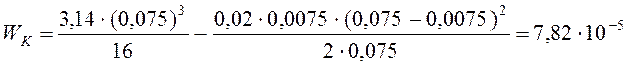 м3
м3
По формуле (3.15)
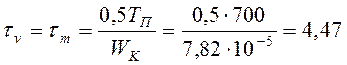 МПа
МПа
Подставляем полученные значения в (4.11) и (4.12):
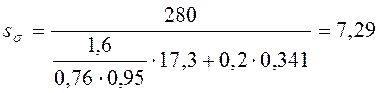
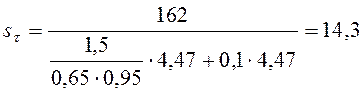
Вычисляем коэффициент запаса прочности (4.9):
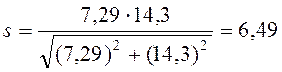
Вывод: условие прочности (4.10) в сечении В – В выполняется:
![]()
5.Проектирование соединений вал-ступица
Проверочный расчёт шпоночных соединений
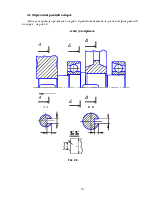
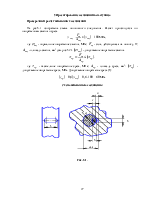
На рис.5.1 изображена схема шпоночного соединения. Расчёт производится по напряжениям смятия и среза
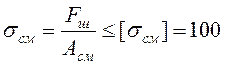 МПа,
МПа,
где ![]() -
нормальное напряжение смятия, МПа;
-
нормальное напряжение смятия, МПа; ![]() - сила,
действующая на шпонку, Н;
- сила,
действующая на шпонку, Н; ![]() - площадь
смятия, мм2 (см. рис.5.2.),
- площадь
смятия, мм2 (см. рис.5.2.), ![]() -
допускаемое напряжение смятия.
-
допускаемое напряжение смятия.
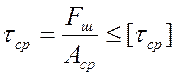 ,
,
где ![]() -
касательное напряжение среза, МПа;
-
касательное напряжение среза, МПа; ![]() - площадь
среза, мм2;
- площадь
среза, мм2; ![]() - допускаемое напряжение
среза, МПа. Допускаемое напряжение среза [1]:
- допускаемое напряжение
среза, МПа. Допускаемое напряжение среза [1]:
![]() МПа
МПа
Схема шпоночного соединения
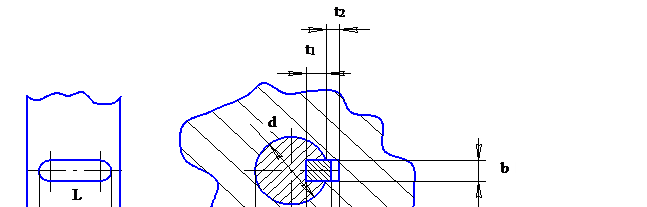 |
Рис. 5.1.
Расчётная схема шпоночного соединения

Рис.5.2.
Площади смятия и среза определяются по
формулам ![]() ,
,
где ![]() -
рабочая длина шпонки, мм;
-
рабочая длина шпонки, мм; ![]() - полная длина
шпонки, мм;
- полная длина
шпонки, мм; ![]() - высота шпонки, мм.
- высота шпонки, мм.
![]()
Сила, действующая на шпонку, определяется по формуле
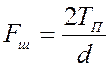
Рассмотрим сечение А – А. Параметры шпоночного соединения:
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм2
мм2
![]() мм2
мм2
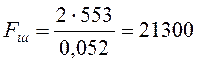 Н
Н
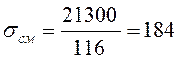 МПа
МПа
![]() МПа
МПа
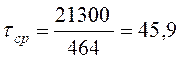 МПа
МПа
![]() МПа
МПа
Вывод: условие прочности по смятию выполняется.
Рассчитываем сечение В – В. Параметры шпоночного соединения:
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм2
мм2
![]() мм2
мм2
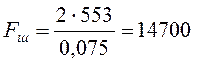 Н
Н
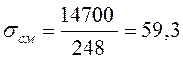 МПа
МПа
![]() МПа
МПа
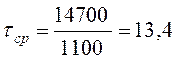 МПа
МПа
![]() МПа
МПа
Вывод: условия прочности по смятию и срезу выполняются.
Проводим расчёты для сечений В-В и Г-Г.
Для сечения В-В условия прочности по смятию и срезу выполняются.
Для сечения Г-Г условия прочности по смятию и срезу не выполняются, поэтому мы установим две шпонки под углом 180º(каждая шпонка будет принимать половину нагрузки)
Проектирование подшипниковых узлов.
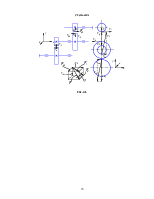
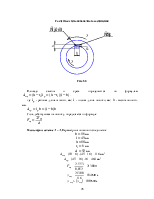
Схема нагружения подшипников
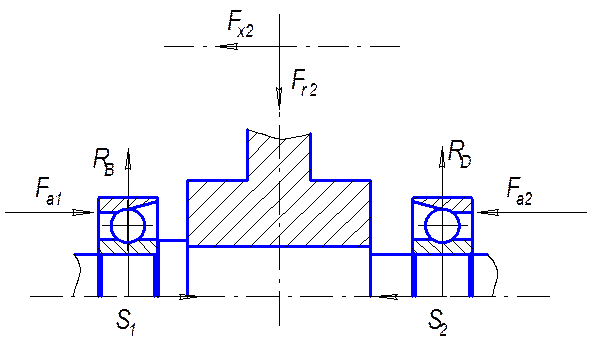
Рис. 4.1.
Необходимо определить ресурс подшипников
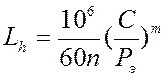 ,
,
где ![]() -
ресурс подшипника, час.;
-
ресурс подшипника, час.; ![]() - частота
вращения одного из колец подшипника, об./мин.;
- частота
вращения одного из колец подшипника, об./мин.; ![]() -
динамическая грузоподъёмность подшипника, Н;
-
динамическая грузоподъёмность подшипника, Н; ![]() -
эквивалентная нагрузка, действующая на подшипник, Н;
-
эквивалентная нагрузка, действующая на подшипник, Н; ![]() -
показатель кривой выносливости,
-
показатель кривой выносливости, ![]() для шариковых
подшипников
для шариковых
подшипников
Если Lh не меньше, чем заданный ресурс- подшипники выбраны верно.
На быстроходном валу поставим подшипники среднй серии(310),а на тихоходном валу – лёгкой серии (213).
СПИСОК ЛИТЕРАТУРЫ
1. Курсовое проектирование деталей машин. Сост. С.А. Чернавский, К.Н. Боков, И.М. Чернин и др. М.:Машиностроение, 1988, 416 с.
2. Егоров В.И., Михайлов Ю.К., Щербак В.Т. Курсовое проектирование по деталям машин с использованием ЭВМ. Учебное пособие. – Л.: изд. ЛПИ, 1982, 76 с.
3. Расчёт радиальных и радиально-упорных подшипников качения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.