Контрольные карты Шухарта с использованием количественных данных. Контрольные карты Шухарта индивидуальных значений

Министерство Образования Российской Федерации

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Механико-машиностроительный факультет

Контрольные карты

Студент:                            

Группа:                               4049/1

Преподаватель:               

САНКТ-ПЕТЕРБУРГ

2006

При помощи контрольных карт Шухарта оценить находится ли технический процесс в статистически управляемом состоянии.

Во многих случаях контрольные карты используются в качестве средства приемки процесса, несмотря на то, что они не разработаны специально как критерии или границы допуска для процесса.

Значения исходной выборки получаем за счет изменения диаметра отверстия: Ø43.  Будем рассматривать 20 подгрупп по 5 наблюдений в каждой подгруппе.

Номер подгруппы	X1	X2	X3	X4	X5
1	43,15	43,09	43,04	43,09	43,10
2	43,14	43,11	43,06	43,09	43,11
3	43,10	43,09	43,07	43,10	43,09
4	43,15	43,11	43,12	43,08	43,14
5	43,09	43,11	43,09	43,14	43,07
6	43,11	43,06	43,15	43,12	43,08
7	43,11	43,10	43,06	43,08	43,10
8	43,06	43,12	43,09	43,12	43,07
9	43,09	43,07	43,09	43,10	43,15
10	43,09	43,11	43,10	43,09	43,06
11	43,10	43,15	43,11	43,07	43,09
12	43,08	43,11	43,10	43,08	43,09
13	43,14	43,09	43,07	43,10	43,10
14	43,13	43,09	43,08	43,10	43,12
15	43,10	43,07	43,15	43,10	43,11
16	43,13	43,09	43,16	43,13	43,06
17	43,10	43,10	43,08	43,11	43,09
18	43,11	43,04	43,13	43,14	43,09
19	43,10	43,11	43,11	43,10	43,10
20	43,07	43,05	43,11	43,08	43,08

Контрольные карты Шухарта с использованием количественных данных.

Для каждой подгруппы считаем среднее значение и размах (табл.2) по формулам:

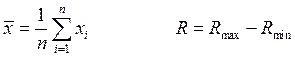, где - среднее значение подгруппы;

x – измеряемая характеристика качества;

n – объем подгруппы, число выборочных наблюдений в подгруппе;

R – размах подгруппы.

Номер	Среднее	Размах	Номер	Среднее	Размах	Номер	Среднее	Размах	Номер	Среднее	Размах
1	43,09	0,11	6	43,11	0,09	11	43,10	0,08	16	43,11	0,10
2	43,10	0,08	7	43,09	0,04	12	43,09	0,03	17	43,10	0,03
3	43,09	0,02	8	43,09	0,06	13	43,10	0,07	18	43,10	0,10
4	43,12	0,06	9	43,10	0,08	14	43,11	0,05	19	43,10	0,02
5	43,10	0,07	10	43,09	0,05	15	43,11	0,09	20	43,08	0,06

Карта Шухарта представляет собой график значений определенных характеристик подгрупп в зависимости от их номеров.

Она имеет центральную линию (cl) соотносительно эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталону обычно служит среднее арифметическое рассматриваемых данных. Также на карте показаны 2 статистически определяемые контрольные границы (ucl и lcl) относительно центральной линии.

Зная стандартные значения (х₀  = 43,1 – средний размер; σ₀ = 0,025 –отклонение процесса), вычислим контрольные границы по формулам:

 - для построения карты размахов;

 - для построения карты средних значений, где Ai,Di – коэффициенты для вычисления контрольных границ, табличные значения.

Получаем для карты размахов:

Получаем для карты средних значений:

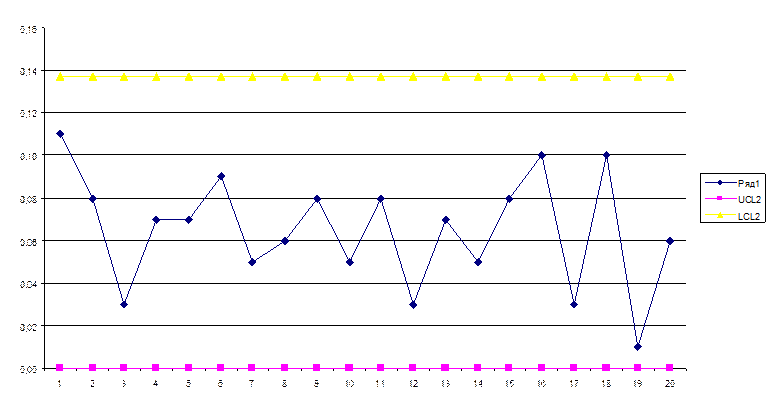
Где 1 – LCL2

2 – значения размахов каждой подгруппы

3 – UCL2

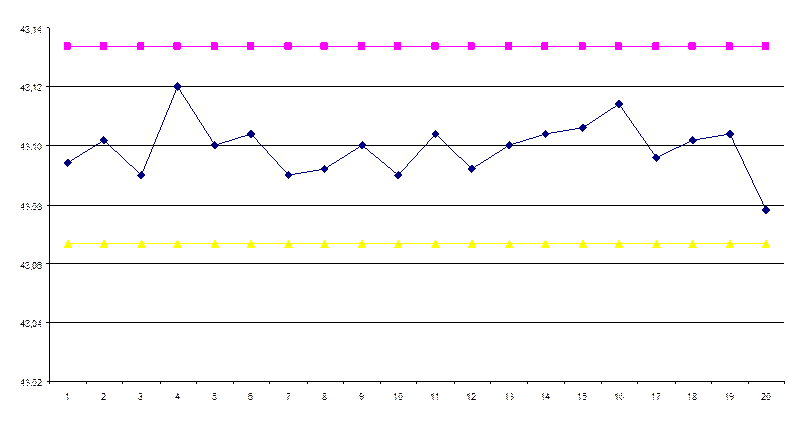
Где 1 – UCL

2 – средние значения диаметральных размеров

3 – LCL

Контрольные карты Шухарта индивидуальных значений.

В некоторых ситуациях невозможно собрать подгруппы, тогда появляется понятие скользящий размах ()– это абсолютное значение разности измерений  в последовательных парах. Т.е. для оценки изменчивости внутри партии рассчитывается по скользящим размахам по 2-м наблюдениям.

Для рассматриваемого наблюдения считаем среднее значение и размах по формулам:     , где - среднее среднего значения первого наблюдения;

x – значения диаметральных размеров;

n – число измерений рассматриваемого наблюдения;

m – количество размахов;

- скользящий размах;

R – значения размахов .

Получаем:

Не зная стандартные значения, вычислим контрольные границы по формулам:

 - для построения карты размахов;

 - для построения карты средних значений, где Ai,Di – коэффициенты для вычисления контрольных границ, табличные значения.

Получаем для карты средних значений (рис.3):

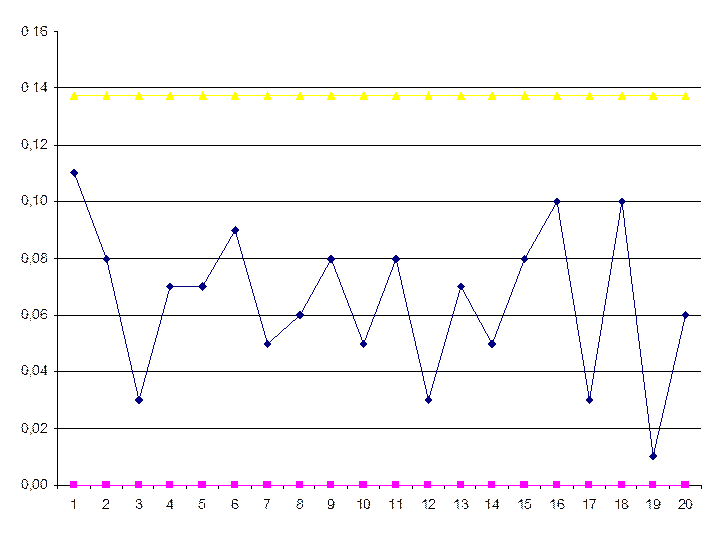
Где 1 – LCL2

2 – значения размахов рассматриваемого наблюдения

3 – UCL2

.

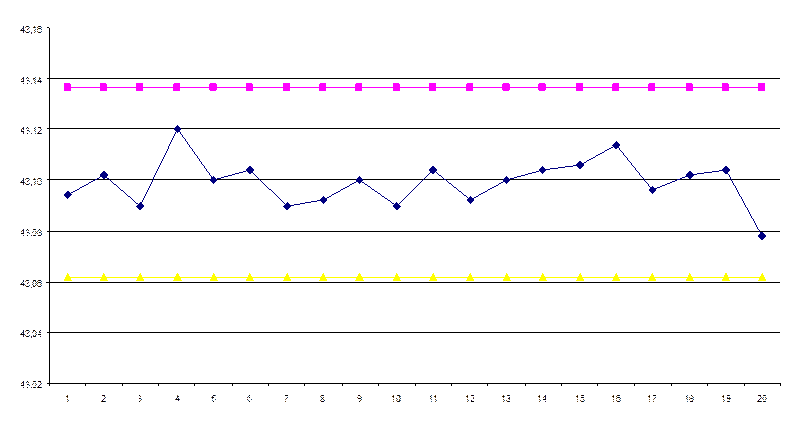Где 1 – UCL1

2 – средние значения диаметральных размеров

3 – LCL1

Получаем:

PCI

0,00105

Вывод: PCI меньше 1, а это означает, что возможности процесса не приемлемы.