Приобретение практических навыков проверки гипотезы о равномерном или нормальном распределении генеральной совокупности по критерию Пирсона

Лабораторная работа №4

Цель работы - приобретение практических навыков проверки гипотезы о равномерном или нормальном  распределении генеральной совокупности по критерию Пирсона

ОСНОВНЫЕ СВЕДЕНИЯ

Чрезвычайно важной задачей сравнительной статистики является сравнение эмпирического и теоретического {или гипотетического) распределений. Если между ними имеется согласие, то можно заключить, что эмпирическое распределение вызвано теми же причинами, которые лежат в основе теоретического распределения. Пригодной для проверки статистикой является величина .

Приближенный критерий проверки гипотезы об отсутствии зависимости основывается на том факте, что малые различия между наблюдаемыми и ожидаемыми числами поддерживают эту гипотезу, а большие отклонения свидетельствуют против нее.

-  Нуль-гипотеза: в основе выборки лежит предполагаемое теоретическое   распределение   Согласно   альтернативной гипотезе выборка принадлежит к неизвестному распределению  

Мы рассматриваем независимую выборку , обозначая неизвестную функцию распределения . Нас интересует вопрос о том, согласуются ли данные наблюдений с простой гипотезой , где - некоторая конкретная фиксированная функция распределения.

Мерой расхождения между теоретическими и эмпирическими вероятностями принимается величина .

Если выборка разделена на  интервалов, причем наблюдаемые значения расположены в отдельных интервалах случайным образом независимо друг от друга, то значение определяется как сумма по всем интервалам квадратов разностей между наблюдаемыми и ожидаемыми частотами, поделенных на ожидаемые частоты.

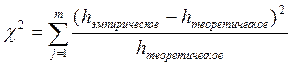, (1)

 - частота попаданий случайной величины в интервал группировки  (наблюдаемая частота);

- теоретическое значение частоты для соответствующего интервала (ожидаемая частота);

- число интервалов группировки.

Статистика называется статистикой  хи-квадрат Пирсона. В случае, если нуль-гипотеза верна,  , если неверна

Теорема К. Пирсона. Предположим, что нуль-гипотеза верна. Тогда при   распределение величины  сходится к распределению хи-квадрат с степенью свобод, где

Минимальное число значений, необходимое для вычисления статистики, называется числом степеней свободы данной статистики,  , где

    - число интервалов выборки;

      - число параметров, оцениваемых по выборке.

Практический смысл теоремы Пирсона состоит в том, что при достаточно большом объеме выборки можно рассчитать статистику , зная значения разностей эмпирических и теоретических значений частот.

То обстоятельство, что поведение существенно различно в зависимости от того верна или нет нуль-гипотеза, дает возможность построить критерий для ее проверки.

Для проверки гипотезы вероятность   ошибки (уровень значимости) задается   заранее.   

При этом, нуль-гипотезу можно:

-  Отклонить, когда , или принять, когда и

Воздержаться, когда и повторить эксперименты для получения большего числа данных.

Наши действия по принятию (или отвержению) нуль- гипотезы  состоят в следующем. Подстановкой имеющихся выборочных данных в формулу (1) вычисляется значение функции , которое затем сравнивается с табличным значением для степеней свободы и принятого уровня значимости:

-  Если значение функции  окажется больше табличного значения , то нуль-гипотеза  отвергается (при этом говорят, что выборка обнаруживает значимое отклонение от нуль-гипотезы);

-  Если значение функции окажется меньше или равно табличного значения , то нуль-гипотеза  принимается (говорят, что выборка совместима с нуль -гипотезой ).

Границы применимости критерия на практике.

Утверждения теоремы Пирсона относятся к пределам при. На практике, конечно, мы имеем дело лишь с выборками ограниченного объема. Поэтому, применяя вышеописанный критерий, необходимо проявлять осторожность. Согласно рекомендациям, применение критерия дает хорошие результаты, когда все ожидаемые частоты . Если же какие-то из этих чисел малы, рекомендуется, укрупняя некоторые группы, перегруппировать данные таким образом, чтобы ожидаемые частоты всех групп были не меньше десяти. Если число достаточно велико (имеет порядок нескольких десятков), то порог для ожидаемых частот может быть понижен до 5 или даже до 3. Ниже представлена-таблица. Структура таблицы такова, что каждая строка относится к определенному числу степеней свободы, а каждый столбец — к определенному вероятностному уровню. Нас интересуют уровни значимости 0,01, 0,05, 0,1, которые соответствуют