Функции распределения. Свойства функции распределения. Плотностью распределения вероятностей непрерывной случайной величины

Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид:

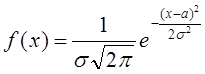
Таким образом, нормальное распределение определяется двумя параметрами: а и σ.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Область определения этой функции: (-∞, +∞).

f(x) > 0 при любом х (следовательно, весь график расположен выше оси Ох), то есть ось Ох служит горизонтальной асимптотой графика при

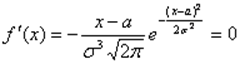
Следовательно, при х = а 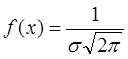 - точка максимума.

f(x – a) = f(a – x), то есть график симметричен относительно прямой х = а.

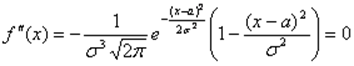
Это условие выполняется в точках перегиба:

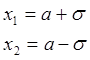
Если случайная величина задана плотностью распределения , то вероятность того, что примет значение, принадлежащее интервалу :

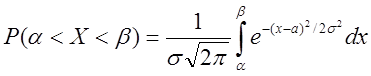
Перед нами так называемый «неберущийся» интеграл, который невозможно выразить через элементарные функции. Поэтому для вычисления значений F(x) приходится пользоваться таблицами. Они составлены для случая, когда а = 0, а σ = 1.

Нормальное распределение с параметрами а = 0, σ = 1 называется нормированным, а его функция распределения -  функцией Лапласа.

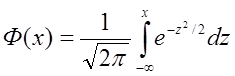
Функцию распределения для произвольных параметров можно выразить через функцию Лапласа, если сделать замену: .

Правило «трех сигм».

Найдем вероятность того, что нормально распределенная случайная величина примет значение из интервала (а - 3σ, а + 3σ):

Следовательно, вероятность того, что значение случайной величины окажется вне этого интервала, равна 0,0027, то есть составляет 0,27% и может считаться пренебрежимо малой. Таким образом, на практике можно считать, что все возможные значения нормально распределенной случайной величины лежат в интервале (а - 3σ,  а + 3σ).

Полученный результат позволяет сформулировать правило «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.

Если имеет распределение нормальное распределение с параметрами , то 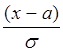 - стандартная нормальная случайная величина.

Квантили распределения

Квантилью уровня a для распределения, порождаемого функцией F(t) называется число , являющееся решением уравнения

Функция F(t)-строго возрастающая; .

Таким образом, квантили – это способ описать группу измерений. Квантили часто называют также процентными точками распределения. 

Квантиль  можно представить точкой  на  числовой  шкале,  которая  делит  совокупность наблюдений на группы с соответствующими пропорциями в каждой из них. Частные случаи квантилей: 

-  Медиана – делит наблюдение на две группы (квантиль порядка 0,5)      

-  Квартиль – делит наблюдения на 4 группы (квантиль порядка 0,25)

-  Дециль – делит наблюдения на 10 групп (квантиль порядка 0, 1)

-  Квинтель – делит наблюдения на 5 групп (квантиль порядка 0,2)

-  Процентиль – делит наблюдения на 100 групп (квантиль порядка 0,01).

Числовые характеристики центральной тенденции

Одной из основных характеристик распределения является тенденция наблюдаемых значений признака группироваться вокруг центра этого распределения. Эта характеристика называется центральной тенденцией. Центральная тенденция обычно выражается тремя способами: средней арифметической, медианой, модой.

Средняя арифметическая  чаще всего используется в качестве числовой характеристики центральной тенденции. Эта характеристика равномерно учитывает значение отклонений и, кроме того, удобна для выполнения различных дополнительных математических операций. Она представляет собой своего рода «центр тяжести» распределения частот; это означает, что алгебраическая сумма всех отклонений от этой средней равна нулю. Формула для определения средней арифметической:

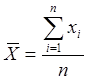, или для упорядоченного ряда  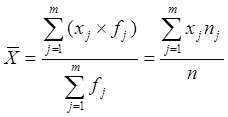, где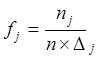

-  - интервал группировки.

-  - частотам попадания наблюдений в интервалы группировки.

Мода – значение признака, которому соответствует наибольшее число наблюдений, или значение признака в наиболее плотном интервале (модальном интервале).

Числовые характеристики рассеяния

Наряду с описанием распределения с точки зрения его центральных тенденций распределение характеризуется рассеянием, или отклонением значений наблюдаемого признака от его среднего значения. Существует несколько видов числовых характеристик рассеяния, среди