1
1. Построение эмпирических функций распределения.
Если случайная величина непрерывна,
то оценка функции распределения ![]() определяется следующим образом. Выборочные
значения
определяется следующим образом. Выборочные
значения ![]() случайной
величины
случайной
величины ![]() располагают в
порядке их возрастания. По этой упорядоченной последовательности
располагают в
порядке их возрастания. По этой упорядоченной последовательности ![]() или вариационному ряду
строят неубывающую ступенчатую функцию:
или вариационному ряду
строят неубывающую ступенчатую функцию:
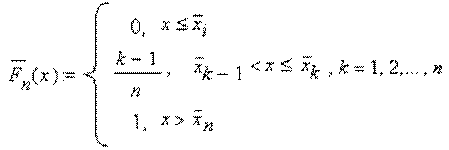
Функцию 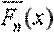 называют эмпирической функцией распределения.
Поскольку эмпирическая функция зависит не только от x, но и от всей
выборки
называют эмпирической функцией распределения.
Поскольку эмпирическая функция зависит не только от x, но и от всей
выборки ![]() , то следует
эту функцию обозначить через
, то следует
эту функцию обозначить через
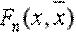
Функцию 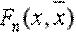 принимают за
оценку теоретической функции распределения F(x).
принимают за
оценку теоретической функции распределения F(x).
Основные сведения:
1. Начальный этап первичной обработки данных связан с поиском
максимального ![]() , минимального
, минимального ![]() значений выборки
значений выборки ![]() и
и
2. размаха варьирования![]() . Для определения
размаха необходимо расположить единицы выборки в возрастающем, или убывающем
порядке.
. Для определения
размаха необходимо расположить единицы выборки в возрастающем, или убывающем
порядке.
3. Следующий этап первичной обработки заключается в группировке данных и их графическом представлении.
4. При группировке промежуток![]() разбивают на m
интервалов и подсчитывают число выборочных значений
разбивают на m
интервалов и подсчитывают число выборочных значений ![]() ,
где j = 1,2,...,m, которые попали в j-й интервал. Как
правило, число интервалов m = 6...20. Для определения оптимального
числа групп можно использовать формулу Стерджесса
,
где j = 1,2,...,m, которые попали в j-й интервал. Как
правило, число интервалов m = 6...20. Для определения оптимального
числа групп можно использовать формулу Стерджесса ![]() ,
где
,
где ![]() - общее число единиц выборки. Величина
интервала группировки
- общее число единиц выборки. Величина
интервала группировки ![]() рассчитывается по
формуле
рассчитывается по
формуле 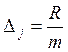 . Ширина интервалов для всего ряда
должна быть одинаковой;
. Ширина интервалов для всего ряда
должна быть одинаковой; ![]() .
.
5. За середину первого интервала ![]() может
быть принято значение
может
быть принято значение ![]() , равное
, равное ![]() ; за середину последнего интервала
значение
; за середину последнего интервала
значение ![]() , равное
, равное ![]() .
.
Тогда
размах варьирования определяется по формуле ![]() (1)
(1)
Каждое отдельное значение ![]() должно быть однозначно отнесено к
определенному интервалу.
должно быть однозначно отнесено к
определенному интервалу.
2.Гистограмма распределения относительных частот. Полигон накопленных частот(кумулятивная кривая)
Наиболее наглядной формой графического представления группировки является гистограмма распределения относительных частот, которая представляет собой график решетчатой функции
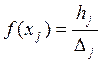 ,
,![]() (2),
где
(2),
где
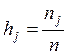 - относительная частота попаданий;
- относительная частота попаданий;
-
![]() -
интервал группировки.
-
интервал группировки.
Другая форма графического представления группированных
данных - полигон частот, который изображается в виде графика - ломаной линии, с
абсциссами ![]() , определяемыми серединами интервалов
группировки
, определяемыми серединами интервалов
группировки ![]() и ординатами, равными частотам
попадания наблюдений в интервалы группировки -
и ординатами, равными частотам
попадания наблюдений в интервалы группировки - ![]() ,
или относительным частотам
,
или относительным частотам 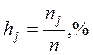 .
.
Пример полигона относительных частот представлен на рис. 1
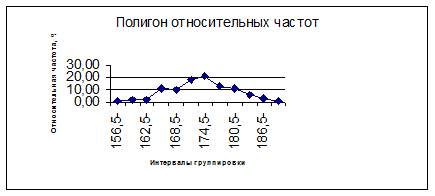
Полигон
накопленных частот (кумулятивная кривая) - график
ломаной линии, с абсциссами ![]() , определяемыми
серединами интервалов группировки
, определяемыми
серединами интервалов группировки ![]() , и ординатами,
равными сумме накопленных частот
, и ординатами,
равными сумме накопленных частот 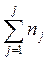 , или сумме относительных
накопленных частот
, или сумме относительных
накопленных частот
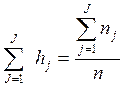 ,% (3).
,% (3).
Пример полигона относительных накопленных частот представлен
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.