МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ И УПРАВЛЕНИЯ
кафедра прикладных информационных технологий
Институт Прикладной информатики
Учебная дисциплина: Информационные технологии
ЛАБОРАТОРНАЯ РАБОТА № 5
Персептрон
Дисциплина: Информационные технологии
Номер группы: 1741
Выполнила:
Номер варианта: 10
Проверила:
Дата регистрации на кафедре: «__»___________2013 г.
Новосибирск – 2013
1.Математическая модель нейрона МакКаллоха-Питса.
Первое систематическое изучение искусственных нейронных сетей было предпринято В.МакКаллохом и В.Питсом в начале 40-х годов. Модель нейрона МаКаллоха-Питса, считается одной из первых моделей нервной клетки. В 1943г. Ученые В.Маккалох и В. Питс разработали систему обработки информации в виде сети, состоящей из простых вычислителей, созданных по принципу биологического нейрона.
Каждый элемент такой сети имеет входы и выходы.
Структурная схема нейрона Маккалоха-Питса представлена на рис.1
 |
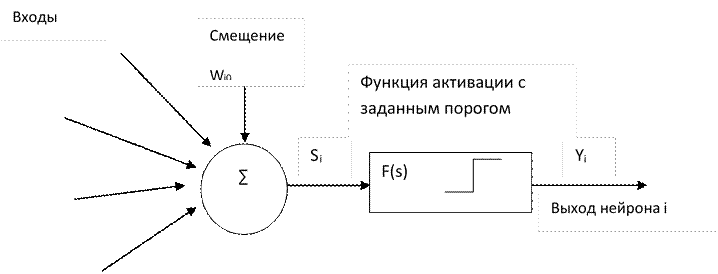Рис.1 Модель нейрона Маккалоха-Питса
Входные сигналы Xi(i=1,2,3… N) суммируются с учетом соответствующих весов синоптических связей Wij в сумматоре, т. е сумматор складывает входные сигналы, взвешенные относительно весов i-го нейрона.
Полученный результат сравнивается с пороговым значение W0 , поступающего с поляризатора. Если сумма больше заданного порогового уровня, то выход равен единице, в противном случае – нулю.
Выходной сигнал yj нейрона рассчитывается по формуле
Yi=f(s) =f
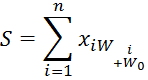
Где f(s) – функция активации нейрона.
Функция активации f(s) ограничивает амплитуду всех выходных сигналов нейрона. Поэтому в литературе она называется функцией сжатия и принимает значения (0,1) или (-1,1).
В
модели МакКаллоха-Питса применяется нелинейная функция активации, пороговая: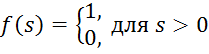 
Выходной сигнал принимает двоичные значения 0 или 1. При этом значение 1 соответствует превышению порога возбуждения нейрона, а значение 0 – возбуждению нейрона ниже порогового уровня. Таким образом, нейрон срабатывает по правилу « все или ничего».
Синапс характеризуется весом или силой на входе сигнал xi, связанный с i-м нейроном, умножается на соответствующий вес.
В отличие от синапсов головного мозга, синоптический вес искусственного нейрона может принимать положительные и отрицательные значения. Положительное значение Wij соответствует возбуждающим синапсам, а отрицательное значение – тормозящим синапсам. При значении Wij=0 между i-м и j-м нейронами связь отсутствует.
Поэтому каждый нейрон можно рассматривать как своеобразный процессор.
Нейрон суммирует сигналы с соответствующими весами, поступающие от других нейронов, выполняет функцию активации и передает результирующее значение связанным с ним нейронам.
Поэтому модель нейрона МакКаллоха-Питса является дискретной моделью, когда состояние нейрона в момент времени (t+1) рассчитывается по значениям его входных сигналов в предыдущий момент времени (t) определяется влиянием остальных нейронов как взвешенная линейная комбинация
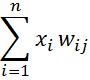
2. Математическая модель и структурная схема простого персептрона.
В 1957 г. Ф.Розенблатт ввел понятие персептрона и правила его обучения.
Персептрон, или простой персептрон (single layer perceptron SLP) – это модель нейрона МакКаллоха-Питса. В 60-е годы персептроны вызвали большой интерес.
Однослойный персептрон можно рассматривать как модель нейрона, состоящую из одного процессора. Сеть состоит из одного нейрона с настраиваемыми весами и порогами ограничений.
Упрощенная схема персептрона представлена на рис.2
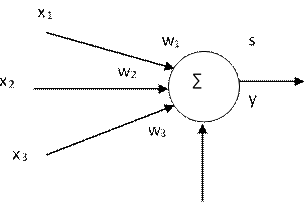Рис.2. Персептрон с тремя входами
Ядро или нейрон имеет три входа (x1,x2,x3),а также вход смещения w0. Каждое соединение от входа к ядру имеет коэффициент – вес (w1,w2,w3),который определяет влияние нейрона на другие нейроны. Веса с положительными значениями оказывают усиление связи, а отрицательные- ослабление связи. В структуре такой сети имеет один выход y.
Функция суммирует все сигналы на входах с учетом весов, затем добавляет смещение. Результат передается в активационную функцию, которая может быть определена как пороговая.
3. Правило обучения персептрона
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.