Персептрон. Математическая модель нейрона МакКаллоха-Питса. Структурная схема нейрона Маккалоха-Питса, страница 2

Процесс обучения персептрона производится с учителем, когда для каждой обучающей выборки, представленной вектором x=[x₀,x₁,x₂,…x_n] (нулевой член вектора x₀=1 формирует сигнал поляризации) ставится в соответствие ожидаемое значение di, получаемое на выходе i-го нейрона. Суть процесса обучения заключается в подборе весовых коэффициентов w_ij , таким образом, чтобы выходной сигнал y_i был близок к ожидаемому значению d_j.

Наиболее популярный метод обучения персептрона заключается в применении правила персептрона.

На начальном этапе обучения весовые коэффициенты w_ij задаются случайным образом.

Шаг 1. На вход нейрона подается обучающий вектор x и рассчитывается значение выходного сигнала y_i . Сравниваются фактически полученные значения y_i  и ожидаемые значения d_i . По результатам сравнения уточняются весовые коэффициенты. Возможны три случая:

А) если y_i = d_i если полученное значение совпадает с ожидаемым, то весовые коэффициенты wij не изменяются;

Б) если y_i=1 и d_i=0, то значения весов уточняются по формуле

В) если y_i=0 и d₁=1 , то значения весов уточняются по формуле

Шаг 3. После завершения уточнения весовых коэффициентов предоставляется следующий обучающий вектор x и связанное с ним ожидаемое значение di и обучение повторяется с шага 2.

Процесс обучения повторяется многократно на всех обучающих выборках, пока различия между yi и di не будут минимальными. Целевая функция E – функция ошибки определяется по формуле:

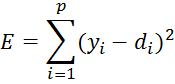
Где p – количество обучающих выборок

Правило персептрона – это частный случай правила Видроу-Хоффа, а в соответствии, с которым изменение весовых коэффициентов нейрона производится по формулам:

При d_i равным 0 или 1, то формуле (2) принимает вид правила персептрона.

4. Правило обучения Видроу-Хоффа для обучения персептрона.

Алгоритм обучения ИНС, основанный на дельта-правиле Видроу-Хоффа состоит в последовательном выполнении шагов:

Шаг 1. На начальном этапе обучения ИНС назначаются случайным образом небольшие значения для весовых коэффициентов (W_ij). Этот этап называют инициализацией весовых коэффициентов.

Шаг 2. На вход сети последовательно подается очередной обучающий вектор x(t)={x₁(t),x₂(t),x₃(t),…x_n(t)}, где t – номер итерации процесса обучения персептрона.

Для каждого нейрона в сети вычисляется взвешенная сумма произведений входных сигналов на соответствующие весовые коэффициенты и применяется пороговая функция активации.

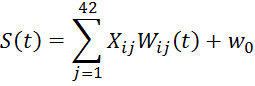
Шаг 3. Выполняется подстройка весовых коэффициентов:

Шаг 4. Производится оценка работы сети и алгоритм повторяется с шага 2.

Расчетная часть.

с коэффициентом 1

x=[1 1 0 0 -1; 1 0 0 1 -1; 0 0 1 1 -1; 0 1 1 0 -1]

weight=[0.4 0.3 0.5 0.2 0.3; 0.4 0.5 0.4 0.3 0.2]

y=[1 1; 1 0; 0 1; 0 0]

koeff=1

iteration=1

S0=0

for t =1:iteration

for i = 1:4

S1=0

S2=0

for j = 1:5

S1=S1+x(i,j)* weight (1,j) ;   %S1=0.5

S2=S2+x(i,j)* weight (2,j);   %S2=0.7

End % применяем правило обучения персептрона – правило Видроу-Хоффа

deltaW = koeff*(y(i,1)-sign(S1))*x(i,:);

sreS1=S0-koeff*(y(i,1)-sign(S1))

weight(1,:) = weight(1,:) + deltaW;

deltaW = koeff*(y(i,2)-sign(S2))*x(i,:);

sreS2=S0-koeff*(y(i,2)-sign(S2))

weight(2,:)=weight(2,:)+deltaW;

end

end

weight

Самостоятельная

С коэффициентом 0.5

x=[1 1 0 0 -1; 1 0 0 1 -1; 0 0 1 1 -1; 0 1 1 0 -1]

weight=[0.5  0.4  0.6  0.3  0.4; 0.5 0.6 0.5 0.4 0.3]

y=[1 1; 1 0; 0 1; 0 0]

koeff=0.5

iteration=1

S0=0

for t =1:iteration

for i = 1:4

S1=0

S2=0

for j = 1:5

S1=S1+x(i,j)* weight (1,j) ;   %S1=0.5

S2=S2+x(i,j)* weight (2,j);   %S2=0.7

end

% применяем правило обучения персептрона – правило Видроу-Хоффа

deltaW = koeff*(y(i,1)-sign(S1))*x(i,:);

sreS1=S0-koeff*(y(i,1)-sign(S1))

weight(1,:) = weight(1,:) + deltaW;

deltaW = koeff*(y(i,2)-sign(S2))*x(i,:);

sreS2=S0-koeff*(y(i,2)-sign(S2))

weight(2,:)=weight(2,:)+deltaW;

end end

weight

С коэффициентом 0.8

x=[1 1 0 0 -1; 1 0 0 1 -1; 0 0 1 1 -1; 0 1 1 0 -1]

weight=[0.5  0.4  0.6  0.3  0.4; 0.5 0.6 0.5 0.4 0.3]

y=[1 1; 1 0; 0 1; 0 0]

koeff=0.8

iteration=1

S0=0

for t =1:iteration

for i = 1:4

S1=0

S2=0

for j = 1:5

S1=S1+x(i,j)* weight (1,j) ;   %S1=0.5

S2=S2+x(i,j)* weight (2,j);   %S2=0.7

end

% применяем правило обучения персептрона – правило Видроу-Хоффа

deltaW = koeff*(y(i,1)-sign(S1))*x(i,:);

sreS1=S0-koeff*(y(i,1)-sign(S1))

weight(1,:) = weight(1,:) + deltaW;

deltaW = koeff*(y(i,2)-sign(S2))*x(i,:);

sreS2=S0-koeff*(y(i,2)-sign(S2))

weight(2,:)=weight(2,:)+deltaW;

end

end

weight