Нормы затрат времени для каждого из типов и оборудования на одно изделие. Рассчитать план выпуска изделий

Пусть  - количество изделий вида А,  - количество изделий вида В, которые планируется изготовить.

Тогда прибыль, полученная от реализации выпущенной продукции равна:

Z= .

Переменные ,  должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении предприятия ресурсов оборудования.

На изготовление одного изделия вида А затрачивается 1 (станко-час) на фрезерном оборудовании, тогда на х₁ изделий понадобится  станко-час. На изготовление одного изделия вида В затрачивается 2 станко-час на фрезерном оборудовании, тогда на х₂ изделий понадобится  станко-час. Поскольку в распоряжении предприятия фрезерного рабочего времени имеется не более 18 станко-час., то получим первое ограничение .

Рассуждая аналогично и просматривая вторую строку таблицы, получим ограничение по рабочему времени токарного оборудования  .

Рассуждая аналогично и просматривая третью строку таблицы, получим ограничение по рабочему времени шлифовального оборудования  .

Учтем, что выпуск изделий не может быть отрицательным, получим систему ограничений:

    ,

,

Математическая модель задачи имеет вид

    ,

,

Найдем графическим способом максимум функции .  

Перейдем к системе равенств:

    ,

,

,

Строим в прямоугольной декартовой системе координат прямые.

1.   . Эта прямая проходит через точки:

2. проходит через точку (0; 7) параллельно оси Ох₁.

3. . Эта прямая  проходит через точки:   

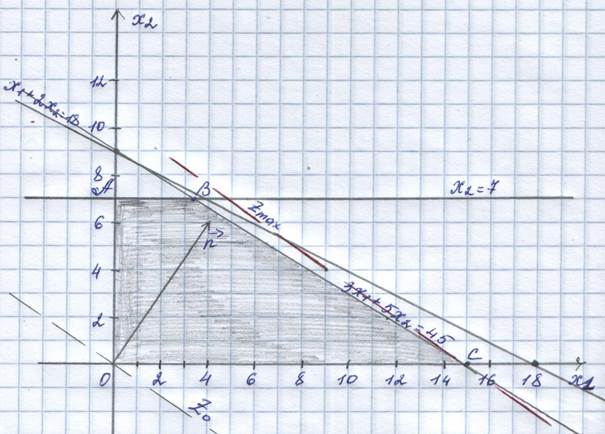
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего  неравенства. Пересечение решений неравенств является решением системы – многоугольником решений.

Возьмем точку (1; 1) и подставим в каждое неравенство системы.

1.  верно. Значит точка (1; 1) принадлежит той части плоскости, которая является решением неравенства .

2. решением неравенства  является часть плоскости расположенная  ниже  прямой .

3.  верно. Значит точка (1; 1) принадлежит той части плоскости, которая является решением неравенства .

Заштриховав соответствующие области, получим многоугольник решений ОАВС.

Строим вектор  с началом в точке (0; 0) и концом в точке (4; 6). Перпендикулярно вектору  через начало координат проводим линию уровня .

Параллельным переносом передвигаем прямую  в направлении вектора  до  последней точки допустимой области, которую линия уровня пересекает при этом движении (линия ). Получим точку С, которая является максимумом.

В точке С пересеклись две прямые: и . Решим систему уравнений этих прямых.

          ,            ,                                                 

 ;                       ,

Получили С (15; 0)

Подставляя координаты точки С в уравнение функции цели, получим:

Z_mах=Z(15; 0)=

Решим задачу симплекс методом.

Задачу необходимо привести к канонической форме, т. е. необходимо перейти от ограничений – неравенств к равенствам. Для этого введем дополнительные (балансовые) неотрицательные переменные: , , .

Поскольку все ограничения имеют знак «», то переменные , ,  берем со знаком «+».

     ,

,

,

Переменные , ,  - означают возможные остатки ресурсов.

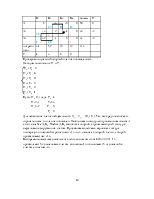
В качестве опорного плана выберем план при котором выпуск продукции не производится и все сырье остается неиспользованным, т. е. Х=(0;  18; 7; 45). Составим симплекс таблицу.

В последней оценочной строке есть отрицательные элементы, поэтому нужно делать шаг симплекс метода. Наибольший по модулю отрицательный элемент (-6) последней строки показывает, что в новый базис следует ввести переменную .Т. е. столбец  является разрешающим. Находим симплекс – отношения: делим элементы столбца «План» на положительные элементы разрешающего столбца и заносим их в последний столбец таблицы «Симплексы». Выбираем наименьшее среди полученных чисел.  Это число 7 стоит во второй строке и соответствует переменной , эту переменную нужно вывести из базиса. Т. е. 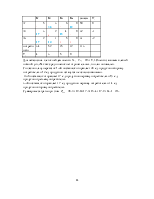строка  является разрешающей. Заполним новую таблицу

В последней оценочной строке есть отрицательные элементы, поэтому