Элементы комбинаторики, размещения, перестановки, сочетания. Упорядоченное множество. Случайные события, алгебра событий, формулы де Моргана

1.  Элементы комбинаторики, размещения, перестановки, сочетания.

Упорядоченное множество – это множество с заданным порядком элементов.

Правило произведения: Пусто А некоторое множество. Пусть элемент а1А можно выбрать n1 способами. После этого а2 можно выбрать n2 способами и тд. Тогда одновременный выбор а1, а2…аn можно сделать n1*n2…*nk способами/

Правило суммы: Пусто А некоторое множество. Пусть элемент а1А можно выбрать n1 способами. После этого а2 можно выбрать n2 способами и тд. Тогда выбор одного из элементов (а1 или а2 или аn) можно сделать n1+n2+…+nk способами.

Размещение из n по k: Размещением из n по k называется каждое упорядоченное подмножество из к элементов, выбранных из n элементов

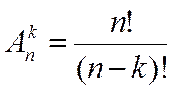
Перестановка – упорядоченное множество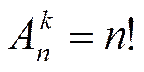

Сочетания – подмножестов из к элементов, выбранных во множестве из n переменных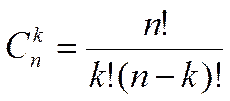

1) 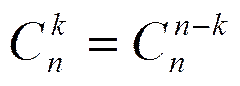           2)

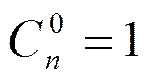
2. Случайные события, алгебра событий, формулы де Моргана.

Событие – исход эксперимента

Эксперимент – создание определенного комплекса условий

Пространство событий – совокупность событий при данном эксперименте

Ø – пустое подмножество(невозможное событие)

Ω -- все множество (достоверное событие)

Несовместные события – события А и В называются несовместными, если они не могут наступить вместе

Противоположные события – это совокупность событий, противоположных А.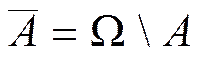(дополнение)

Алгебра событий

А+В=АВ  wA+B ówA V wB

A·B=AB  wA·BówAwB

Свойства операций:

1)  А+В=В+А  2) А*В=В*А  3) А+ =Ω  4) А*Ω=А  5)АВ С А  6) *А= Ø  7) =А   8) А-В=А*  9)   10)

3.Классическая вероятность, теорема сложения вероятностей.

Вероятность события – это число, характеризующее возможность наступления данного события P(A)

Вероятность невозможнгого=0, а достоверного=1. Вероятность любого другого [0,1].

Классическая вероятность – это классическое пространство событий, состоящее из конечного числа элементарных событий и все они равновозможны. P(A)=na/n, где na-благоприятные исходы, n- все возможные исходы

Теорема сложения вероятностей

Если А и В два события, то вероятность их суммы P(A+B)=P(A)+P(B)-P(AB)

Для несовместных событий:

P(A+B)=P(A)+P(B)

Для 3-х: P(A)+P(B)+P(C)-P(AC)-P(AB)-P(BC)+P(ABC)

P()=1-P(A)

4.  Статистическое определение вероятности, геометрическая вероятность.

Пусть при проведении n испытаний, некоторое событие А появилось m раз.Многочисленные эксперименты такого рода показывают, что при больших n отношение m/n, называемое частостью события А, остается примерно постоянным. Статистическое определение вероятности заключается в том, что за вероятность события А принимается постоянная величина, вокруг которой колеблются значения частостей при неограниченном возрастании числа n.

Геометрическая вероятность

Обобщением классической схемы является пространство событий, элементарные исходы которого можно представить в виде точек, заполняющих некоторою область Ω в (трехмерном) пространстве в R³ . Если при этом  событию А благоприятствуют элементарные события, заполняющие некоторую подобласть D из Ω, то геометрической вероятностью события А  называется отношение объема области D к объему области Ω: P(A)=V(D)/V(Ω). Аналогично определяется геометрическая вероятность события, когда множество Ω представляет собой некоторую область на плоскости или отрезок на прямой линии. В этих случаях объемы областей заменяются , соответственно, площадями фигур или длинами отрезков.

5. Аксиоматическое определение вероятностей.

Ω={ω} --  набор элементарных событий

Рассмотрим набор подмножеств F={A/A c Ω}

Аксиома 1: Если А1, А2…Аn…  F => A1+A2+…+An+…  F

Аксиома 2:  Для любого АF =>   F

Любой набор подмножеств данного множества, обладающий свойствами 1 и 2 – σ-алгебра

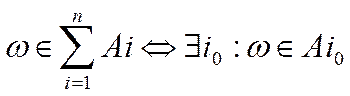
Из этих аксиом следует, что произведение любого подмножества тоже принадлежит σ-алгебре.

Аксиомы вероятностей

Вероятность события АF(A c Ω) называется число  P(A), которое обладает следующими свойствами:

1)  P(Ω)=1 P(A)>=0

2)  Если семейство событий А1, А2…Аn… попарно несовместны, т.е. Ai*Aj=Ø, то вероятность суммы  P(A1+A2+…+An+…)=P(A1)+P(A2)+…+P(An)+…

Дискретное вероятностное пространство --  вероятностное пространство, в  котором пространство событий конечно или счетно, а σ-алгебра F  -- множество всевозможных подмножеств дискретного множества Ω .

6.Условные вероятности и теорема умножения.

На практике часто встречаются ситуации, когда наступление некоторого события значительно меняет возможности наступления других событий и их вероятности. Если произошло событие B, то новая вероятность события А называется условной вероятностью и обозначается P_B(A), говорят: «вероятность события А при условии B». При этом B оказывается достоверным событием и играет роль пространства элементарных событий Ω.

Условная вероятность P_B(A) определяется формулой (при P(B) >0):

P_B(A)=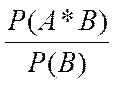 (1)

Из (1) следует формула:

P(A*B)= P_B(A) P(B), P(B)>0,  (2)

И симметричная формула:

P(A*B)= P_A(B)P(A), P(A)>0     (3)

Независимыми называются такие события