Расчет базовых параметров, определяющих качество передачи информации по каналу с помехой. Расчет пропускной способности канала с помехой, страница 5

H(x_i)= -P_io*log₂P_io- P_i1*log₂P_i1.

Этот метод извлечения максимальной информации о состоянии объекта при каждом шаге проверки. Это требует проверки того параметра, который имеет max энтропию H(x_i) при данном опыте, что соответствует min разности ΔP_i=P_io- P_i1.

На первом этапе составляется таблица вероятностей P_io, P_i1 и их разностей по формулам (1)и(2).

Вероятности	x1	x2	x3		xm
Pio	P10	P20			Pm0
Pi1	P11	P21			Pm1
ΔPi	ΔP1	ΔP2			ΔPm

Например, для параметра x₄ прежней таблицы (*)

	1
	0
	1
	0
	1
	0

Обозначим суммарные вероятности через P₁₁(x₁=1)=P₁+P₅+P_N…;P₂₀=P₅+P_j…

Определяются разности

НАПРИМЕР:  или возможно 

На основании min разностей строится алгоритм поиска<при >

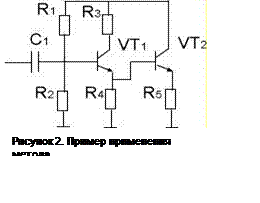
                   Таблица 1,2

Неисправности	n1	n2	n3	n4	n5	n6	n7
Вид неисправности	R1	R2	R3	R4	C1	VT1	VT2
Вероятность	0,1	0,07	0,08	0,20	0,11	0,09	0,35
Параметры
Uб1   x1	0	0	0	1	0	0	0
Uk1  x2	0	1	0	1	0	0	0
Ik1  x3	0	1	0	1	1	0	0
Iэ1  x4	0	1	0	0	1	1	0
Uб2  x5	0	1	1	0	1	0	1
Uэ2  x6	0	1	1	1	1	1	0

Таблица 3

Анализ разностей вероятностей событий показывает, что наиболее информативной позицией является шестая и  тест следует начинать с контроля параметра x₆(U_э2).

Далее определяются условные вероятности: P_i1(x₆=1); P_i0(x₆=1); P_i1(x₆=0); P_i0(x₆=0) и делается анализ разностей взаимноинверсных событий. На основе этого анализа строится дальнейшая трассировка алгоритма поиска. Например, при значении параметра x₆=1 следует тестировать параметры x₂ и x₄, а при x₆=0 - следует перейти к параметру x₅.

Т.е определяем P_i0 и P_i1 при x₆=0

Далее тестирует параметры x_1,4,5 при x₂=1 и x₃ при x₂=0. Т.о.