Расчет базовых параметров, определяющих качество передачи информации по каналу с помехой. Расчет пропускной способности канала с помехой, страница 4

Если критерием является время(быстродействие), то оценка

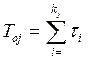- полное время идентификации неисправности. Если все интервалы времени одинаковы и все τ_i=τ_x, тогда полное время идентификации T_oj=k_jτ_x.

Чем меньше параметров k_j, тем выше скорость идентификации неисправности.

Таким образом, критерием качества многофакторной диагностики является минимум среднего времени отыскания неисправности.

Общее число возможных кодовых групп, которыми можно закодировать неисправности, определяется числом контролируемых параметров m, комбинирующихся в различных сочетаниях от 1 до m.

.

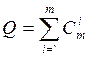Т.е. задача заключается в построении кода неисправности с минимумом средней длительности кода на основе оптимального алгоритма(последовательности диагностических шагов). Длительность кодовый группы при этом определяется приростом информации каждого этапа проверки.

Правило: Чем значительнее прирост, тем короче кодовая группа.

Неопределённость результата проверки определяется энтропией

H=- P_io*log₂P_io- P_i1*log₂P_i1

(Вероятности P_io и P_i1 определяются выражениями (1),(2)).

H_max  достигается при равенстве значений P_io ≈P_i1

Вариантом синтеза оптимального алгоритма является применение метода Шеннона-Фано. При этом выявляются:

- неисправности с суммарными вероятностями близкими к 0,5, при этом выбирается параметр, создающий исход близкий к “1”  и создающий исход близкий к “0”

- выделяется подгруппа с вероятностями P≈0,5 c выявлением аналогичных тенденций к “1” и “0”; - затем группы разбивается на подгруппы с P≈0,125

- разбиение на подгруппы продолжается до тех пор, пока группа не будет содержать 2 параметра.

Вариант синтеза кодов оптимального алгоритма

А -  неисправности, В – их вероятности; С – параметры, выбираемые для проверки

3.2 Информационный метод анализа

Заключается в определении информативных характеристик элементов