Теорема
Котельникова В.А. (1933 г., К. Шеннон 1949 г.) определяет минимальную частоту
следования отсчетов непрерывного сигнала, спектр которого ограничен частотой fв,
при которой в принципе возможно восстановление сигнала по отсчетам абсолютно
точно: ![]()
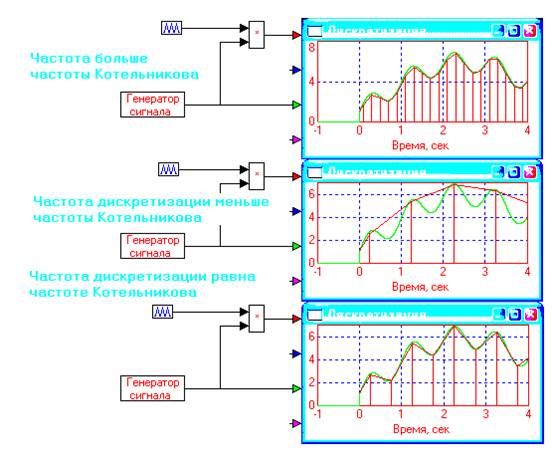
Дискретизация с частотой Котельникова и выше позволяет восстановить непрерывный сигнал точно, а с частотой меньшей - не позволяет.
При сравнительно низкой частоте дискретизации, определяемой теоремой Котельникова, трудно технически восстанавливать сигнал: требуется фильтр с переходной функцией вида (sin x)/x, реализуемый приближенно и только с запаздыванием.
Однако если есть возможность, то частоту дискретизации можно увеличить на порядок или больше и тогда восстановление непрерывного сигнала упрощается, поскольку можно использовать достаточно простой фильтр, сохраняющий значение величины дискреты до появления следующей . Для этого можно просто подать импульсную последовательность на фильтр нижних частот (ФНЧ) с соответствующим коэффициентом усиления.
Устройство, стробирующее непрерывный сигнал импульсом единичной площади, называется дискретизатор, а сохраняющее значение площади на время промежутка между дискретами -фиксатор.
11.4 Выбор шага квантования
Ошибка квантования определяется его шагом. Зная точность, с которой нужно восстанавливать непрерывный сигнал, можно выбрать шаг квантования уровня сигнала меньшим, чем допустимая ошибка при восстановлении непрерывного сигнала.
Обработка отсчетов непрерывного сигнала, представленных в числовой форме, не представляет существенных трудностей для цифрового процессора и может осуществляться с любой требуемой точностью. Поэтому при изучении САР с цифровым управлением основное внимание уделяется вопросам описания и анализа процесса сопряжения непрерывного сигнала с амплитудно-модулированной последовательностью импульсов, представляющих собой результат дискретизации, а также сопряжения результата восстановления дискрет после обработки в цифровом процессоре, с непрерывной частью САР.
САР, в которых в отдельных точках ветвей структурной схемы имеются дискретизированные сигналы, называются амплитудно-импульсными (АИСАР). Математически такие САР описываются с помощью аппарата Z-передаточных функций.
Типовая ветвь АИСАР(рис.11.4) состоит из дискретизатора (идеального импульсного элемента - ИИЭ), фиксатора и непрерывной части:
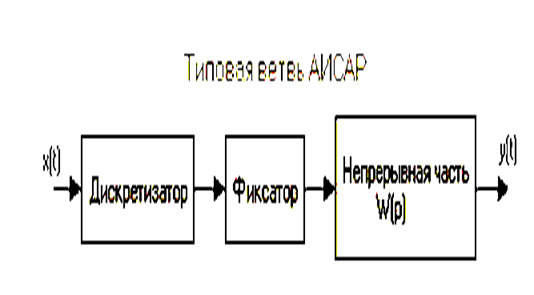
Любое непрерывное звено САР может быть заменено типовой ветвью АИСАР и наоборот: выходные сигналы исходной ветви непрерывной САР и эквивалентной ей ветви АИСАР практически совпадают. Замена эквивалентна, если частота дискретизации значительно (на порядок и более) выше частоты Котельникова, а также если период дискретизации значительно (в 2 - 10 раз и более) меньше наибольшей из постоянных времени непрерывной части
Главное преимущество представления непрерывного звена или ветви САР в виде типовой ветви АИСАР состоит в том, что преобразование сигнала последней можно реализовать в виде программного алгоритма. А результаты вычислений затем можно легко сопрячь с непрерывной частью.
Для математического описания амплитудно-импульсных АИСАР используется Z-преобразование.
Z-преобразование ставит во взаимнооднозначное соответствие результату дискретизации непрерывного сигнала (т.н. решетчатой функции) некоторую функцию комплексной переменной z:
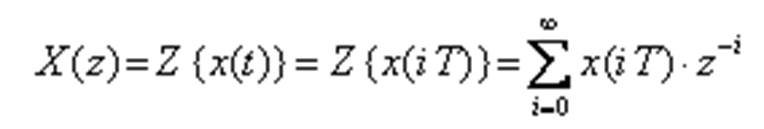
Где
x(iT) - значения амплитуд дискрет, полученных в результате дискретизации непрерывного сигнала.
Правая часть представляет собой бесконечный ряд, сходящийся к функции X(z).
Z-преобразование - линейное.
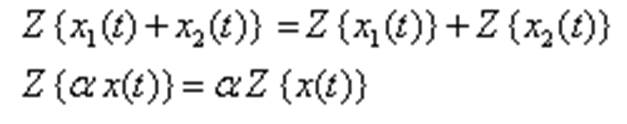
Обратное Z-преобразование Z-1{X(z)} позволяет по Z-изображению X(z) получить оригинал, т.е. решетчатую функцию x(iT), сгладив которую можно получить непрерывный сигнал.
Типовая ветвь АИСАР описывается дискретной Z-передаточной функцией:
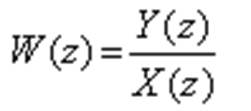
Формально, эта передаточная функция связывает решетчатую функцию выходного сигнала с решетчатой функцией входного.
Переход от непрерывной системы к системе дискретной во времени дает подстановка Тастина:
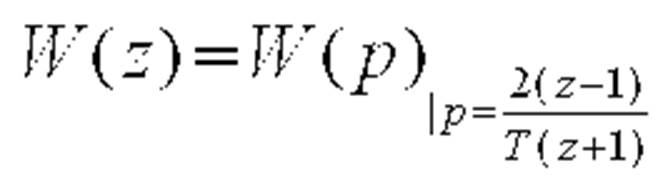
Коэффициенты полиномов числителя и знаменателя Z-передаточной функции конкретной АИСАР зависят от периода дискретизации. Поэтому даже при небольшом изменении значения периода будут получаться другие выражения для передаточной функции, но описывать они будут ту же самую непрерывную ветвь или АИСАР целиком.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.