Исследование свойств типовых сигналов ИИС. Определение программной погрешности результата спектрального анализа типовых сигналов ИИС, страница 2

Динамические искажения связаны с тем, что в момент каких–либо переключений в ИИС возникает преобразование энергии электрического поля в энергию магнитного поля. Эти внутренние процессы внутри схем ИИС накладываются на полезный сигнал и изменяют его до неузнаваемости. Чтобы этого не было, указывается время начала отсчета измерений, за которое динамические переходные процессы практически затухли.

Перекрестные искажения в приемниках. Вызваны тем, что приемники обмениваются своими сигналами по «паразитным связям». Это приводит к возникновению помехи, которая ухудшает прием полезной информации.

Существуют и другие искажения сигналов, вызванные взаимосвязью передатчиков полезной информации.

6   Сравнение формы сигналов по результатам разложения в ряд Фурье

Итак, названные нами причины приводят к искажению формы сигналов, которые несут в себе данные, адреса или команды. Это приводит к погрешности измерений и даже к аварийным ситуациям в самой ИИС. Спектральный состав сигналов позволяет выявить это отличие и, тем самым, сделать вывод о идентичности формы сигналов или их большом различии. Так как описание реальных сигналов абсолютно точки сделать невозможно, то можно использовать метод композиции [8] выходных сигналов.

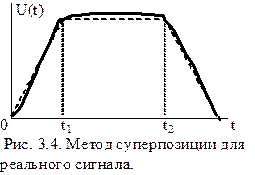Например, выходной сигнал похож на трапецию (рис. 3.4, сплошная линия). Тогда разбивают этот сигнал на три составляющие:

·  первый сигнал, для времени, представим, как линейно нарастающий сигнал (рис. 3.4), который легко разложить в ряд Фурье;

·  для интервала времени, представим во времени реальный сигнал как П-образный идеальный сигнал, который тоже легко разложить в ряд Фурье;

·  третья часть сигнала это линейно-убывающий сигнал.

Разложив эти сигналы в ряд Фурье, выберем существенные гармоники (сильно искажающие форму выходного сигнала относительно формы входного сигнала) и запищем спектральный состав реального сигнала как сумму выбранных нами гармоник. В результате получим спектр, который можно сравнить со спектром входного сигнала, и тем самым, указать на степень расхождения формы входного и выходного сигналов.

7   Задание

7.1   Получить у преподавателя параметры сигналов для исследования их спектрального состава.

7.2   Рассчитать 5 гармоник этих сигналов математическими средствами.

7.3   Провести эксперимент с помощью программы spektoanalizator. Сравнить теоретического расчета и выходные результаты работы программы.

7.4   Провести эксперимент с помощью программы Mathcad. Сравнить полученные результаты с уже имеющимися данными.

7.5   Сделать вывод о потенциальных возможностях применяемых программ, и дать им оценочную характеристику.

8   Содержание отчета

8.1   Титульный лист.

8.2   Цели и задачи лабораторной работы.

8.3   Математический расчет гармоник спектра сигнала, предложенного преподавателем или выбранного из таблицы  3.1 приложения 1.

8.4   Результаты эксперимента с помощью программы spektoanalizator.

8.5   Результаты эксперимента с помощью программы Mathcad.

8.6   Рекомендации и выводы  о возможностях программ.

8.7   Рекомендации по использованию иных программ, применяемых в ИИС  для спектрального анализа  сигналов.

Приложение 1. Варианты для выбора типа сигналов П-образного и линейно-нарастающего.

Таблица 2.1. Таблица для выбора информационного сигнала по своему варианту.

Вариант	1	2	3	4	5	6	7	8	9	10
Длительность сигнала	0,2…0,4	0,2…0,4	0,2…0,4	0,2…0,4	0,2…0,4	0,2…0,4	0,2…0,4	0,2…0,4	0,2…0,4	0,2…0,4
Скважность	5	10	15	20	25	30	35	40	45	50
Амплитуда	8	6	4	2	1	8	6	4	2	1
Вид сигналов	2	3	4	5	6	7	8	9	10	11

В таблице 2.1 форма сигналов помечена символами следующим образом:

·  пилообразный сигнал – 1, П-образный сигнал – 2;

·  форму 3 сигнала на рис. 3.4 взять от начала координат до момента ;

·  форму 4 сигнала на рис. 3.4 взять от момента ;

·  форму 5 сигнала на рис. 3.4 взять полностью;

·  форму 6 сигнала взять треугольной формы (на рис. 3.4 без средней части);

·  форму 7 сигнала взять так: для времени  П-образная ступенька, напряжение которой в 2 раза меньше ступеньки для времени ;

·  форму 8 сигнала взять так: для времени  П-образная ступенька, напряжение которой в 2 раза меньше ступеньки для времени ;

·  форму 9 сигнала взять так: для временных отрезков  и  П-образные ступеньки, напряжение которых в 2 раза меньше ступеньки для времени ;

·  форма 10 получается из рис 3.4 следующим образом: для времени  П-образная ступенька, напряжение которой в 2 раза меньше ступеньки для времени , остальные части сигнала рис. 3.4 сохраняются;

·  форма 11 получается из рис. 3.4 следующим образом: для времени  П-образная ступенька, напряжение которой в 2 раза меньше ступеньки для времени , остальные части сигнала рис. 3.4 сохраняются.

Литература

Дополгительная

1.   Жук В.В., Натансон Г.И. Тригонометрические ряды Фурье и элементы теории аппроксимации. — Л.: Изд-во Ленингр. ун-та, 1983. — С. 188.