Исследование свойств типовых сигналов ИИС. Определение программной погрешности результата спектрального анализа типовых сигналов ИИС

Лабораторная работа №2

Исследование свойств типовых сигналов ИИС

Цель работы:

-  Ознакомится с основными сигналами ИИС.

Задачи:

-  изучить общий метод сравнения формы сигналов;

-  получить навыки математической обработки различных сигналов с помощью рядов.

-  научиться методом разложения функции в ряд Фурье определять спектральный состав исследуемых сигналов ИИС;

-  получить навык определения программной погрешности результата спектрального анализа типовых сигналов ИИС.

1  Введение в тригонометрический ряд Фурье

Огромное число явлений природы изменяется периодически, их можно описать синусоидальной функцией. Однако в процессе взаимодействия объектов вселенной синусоидальные процессы оставляют на объектах следы взаимодействия,  которые будут периодическими, но несинусоидальными. Так открывается понятие того, что практически любой периодический несинусоидальный сигнал (функция) можно представить в виде суммы тригонометрических функций. Такую сумму тригонометрических функций (гармоник) принято называть  рядом.

Тригонометрическим рядом Фурье функции   называют функциональный ряд вида

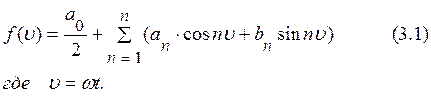
Здесь коэффициенты ряда вычисляются по формулам

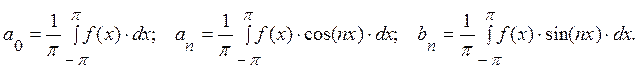
В измерительной технике в качестве переменной  используют текущую фазу  электрических сигналов. При этом вычисленные  коэффициенты разложения в ряж Фурье позволяют вычислить амплитуду гармоник, входящих в периодический (и не периодический) рассматриваемый нами сигнал.

.

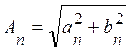Для удобства проведения математических операций над гармониками ряда Фурье выражение (3.1) записывают в комплексной плоскости в следующем виде

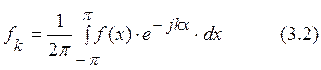
В выражении (3.2) степенная функция   определяет единичный вектор направления колебаний гармоник в трехмерном пространстве. Используя для расчета гармоник формулу (3.2), получим коэффициенты разложения функции в ряд Фурье в комплексном виде

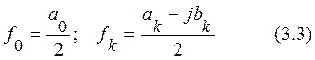
Выражения (3.3) позволяют взять модуль от коэффициентов, а корень квадратный из модуля, умноженный на два, даст нам амплитуду  гармоники.

2  Программа разложения сигналов в ряд Фурье

Программа spektoanalizator запускается в работу обычным образом. При этом на экране монитора появляется окно настроек сигналов.

·  Свойства сигнала позволяет менять временной шаг дискретности в интервале, при этом автоматически меняется масштаб времени по оси абсцисс.

·  Период сигнала лучше всего менять в пределах интервала.

·  Амплитуду исследуемого сигнала можно менять в интервале.

·  Скважность сигнала программа разрешает устанавливать в пределах . При выбранной большой скважности можно считать импульсы одиночными.

·  Количество гармоник устанавливает оператор по своему усмотрению так, чтобы на экране виртуального спектроанализатора уместилось нужное число гармоник.  

3  Программа генерации вариантов разложения функции в ряд Фурье

Программа generator_variantov для проверки правильности работы программы и по усмотрению преподавателя может быть использована для раздачи вариантов расчета гармоник сигналов студентам. Это не исключает выдачу иных заданий, не предусмотренных в отмеченной нами программе. Программа автоматически вычисляет коэффициенты ряды Фурье, и амплитуды гармоник, начиная с первой гармоники.

4   Разложение в ряд Фурье с помощью программы Mathcad

Программа Mathcad позволяет провести разложение функции в ряд Фурье, если ее описать математической формулой. Заводим вместо формулы предыдущей работы (в окне ранее работали с функцией  ) свою функцию  (сигнал). Например, прямоугольный импульс можно задать такой записью: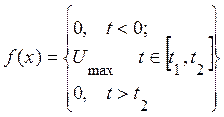

После анализа сделанной записи приходим к выводу о том, что интегрировать нужно функцию, а пределы интегрирования установить от до . Аналогично можно сделать запись для линейно нарастающего сигнала и определить как выражение для самой функции, так и определить пределы ее интегрирования.

Теперь можно  из группы инструментов "Evaluate toolbar" выбирать команду "Evaluate symbolically" и в открывшемся окне рис. 3.1 сделать запись своей функции для вычисления коэффициента разложения функции в ряд Фурье.

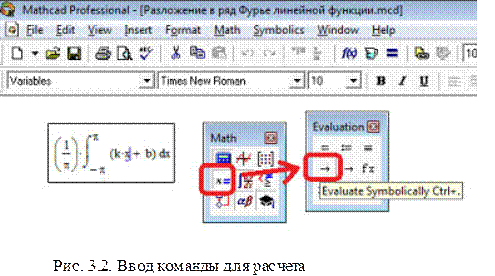Далее, как показано на рис. 3.2, вводим команды для расчета. Если выбрать команду "Evaluate symbolically", то результат вычислений получим в символической форме.

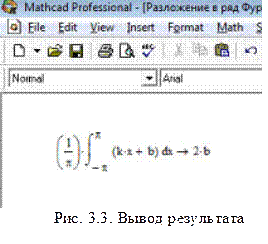В окне 3.3 появляется результат  расчета. Если сказано, сколько гармоник следует вычислить, то в поле ввода данных следует записать выражения для вычисления коэффициентов разложения в ряд Фурье. Затем вычислить амплитуды нужных нам гармоник. Если результаты расчета при домашней подготовки и в отмеченных программах одинаковы, то эксперимент следует считать успешным (при заданной неопределенности измерений).

5   Понятие реальных и идеальных сигналов реального мира

Электрические сигналы используют в ИИС в качестве переносчиков данных, адресов, команд. Если предположить, что мы получили идеальные сигналы, то в процессе их транспортировки сигналы искажаются.

Нелинейные искажения. Этот вид искажений вызван тем, что электронные блоки имеют явно нелинейную зависимость выходного сигнала от входного. В результате в сигнале появляются паразитные гармоники, и форма сигнала изменяется.

Частотно-фазовые искажения. Эти искажения вызваны тем, что в каналах преобразования синалов присутствуют элементы, преобразующие электрическую энергию в энергию электростатического и магнитного полей. В результате на разных частотах входного сигнала выходной сигнал усиливается или уменьшается , хотя входной сигнал к этому не предрасположен. Форма выходного сигнала становится искаженной по сравнению с формой входного сигнала. Если сигнал имеет множество гармоник, то разные гармоники меняют фазу в выходном сигнале, что тоже приводит к значительному изменению формы выходного сигнала.