







ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра “Вагоны и вагонное хозяйство”
Отчет
по лабораторной работе “Автомат”
Выполнил
студент гр. В-008
Афанасьев А.Е.
Проверила
Чистосердова И.Э.
Санкт-Петербург
2004
Проверка качества и оценка устойчивости системы автоматического управления
креном кузова вагона.
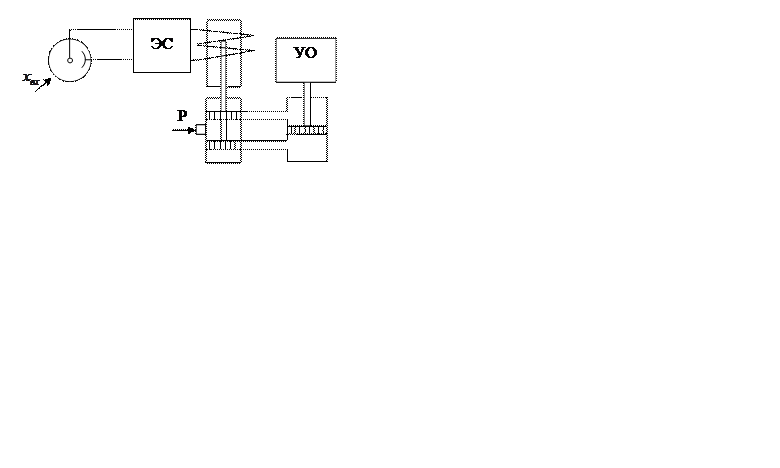
Рис.1. Принципиальная схема системы автоматического
управления наклоном кузова вагона.
Выбор параметров элементов САУ
1. Воспринимающий блок.
Фотоэлемент – безынерционное звено
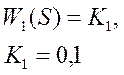
2. Преобразующий блок.
Соленоид – колебательное звено
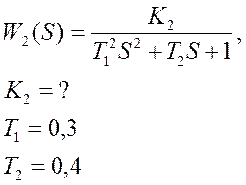
3. Усилительный блок.
Гидравлический усилитель – безынерционное звено
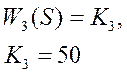
4. Исполнительный блок.
Гидравлический поршневой двигатель – интегрирующее звено
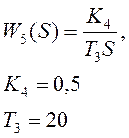
5. Управляемый объект.
Тележка - инерционное
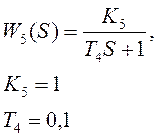
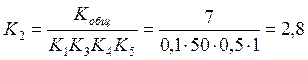
Характеристики звеньев сведем в таблицу 1.
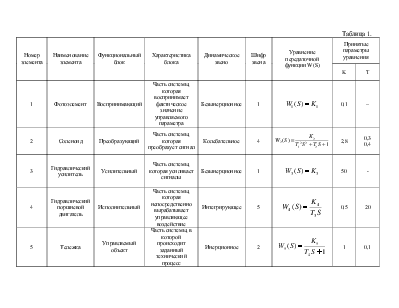
Таблица 1.
|
Номер элемента |
Наименование элемента |
Функциональный блок |
Характеристика блока |
Динамическое звено |
Шифр звена |
Уравнение передаточной функции W(S) |
Принятые параметры уравнения |
|
|
K |
T |
|||||||
|
1 |
Фотоэлемент |
Воспринимающий |
Часть системы, которая воспринимает фактическое значение управляемого параметра |
Безынерционное |
1 |
|
0,1 |
– |
|
2 |
Соленоид |
Преобразующий |
Часть системы, которая преобразует сигнал |
Колебательное |
4 |
|
2,8 |
0,3 0,4 |
|
3 |
Гидравлический усилитель |
Усилительный |
Часть системы, которая усиливает сигналы |
Безынерционное |
1 |
|
50 |
- |
|
4 |
Гидравлический поршневой двигатель |
Исполнительный |
Часть системы, которая непосредственно вырабатывает управляющее воздействие |
Интегрирующее |
5 |
|
0,5 |
20 |
|
5 |
Тележка |
Управляемый объект |
Часть системы, в которой происходит заданный технический процесс |
Инерционное |
2 |
|
1 |
0,1 |
Математическая модель САУ
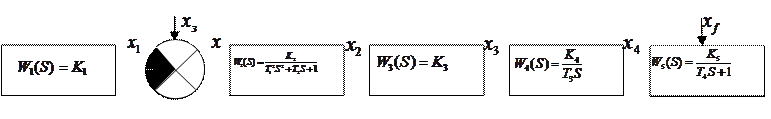 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
Рис.2. Структурная схема системы автоматического
управления углом поворота тележки.
![]()
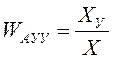
![]()
![]()
![]()
![]()
![]()
Полином полученный при ![]() это собственное движение
системы
это собственное движение
системы
Разрешим относительно ошибки
![]()
![]()
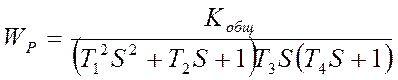
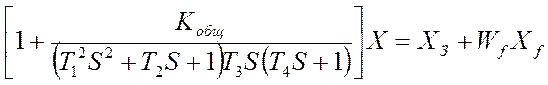
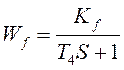
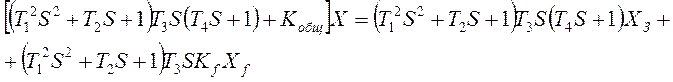
![]()
![]()
![]()
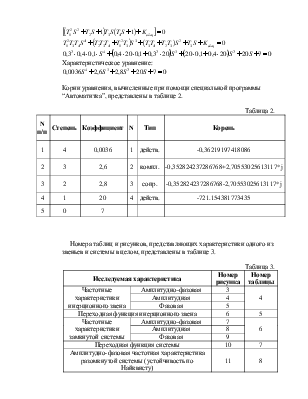
Характеристическое уравнение:
![]()
Корни уравнения, вычисленные при помощи специальной программы
“Автоматитка”, представлены в таблице 2.
Таблица 2.
|
N п/п |
Степень |
Коэффициент |
N |
Тип |
Корень |
|
1 |
4 |
0,0036 |
1 |
действ. |
-0,36219197418086 |
|
2 |
3 |
2,6 |
2 |
компл. |
-0,352824237286768+2,70553025613117*j |
|
3 |
2 |
2,8 |
3 |
сопр. |
-0,352824237286768-2,70553025613117*j |
|
4 |
1 |
20 |
4 |
действ. |
-721.154381773435 |
|
5 |
0 |
7 |
Номера таблиц и рисунков, представляющих характеристики одного из звеньев и системы в целом, представлены в таблице 3.
Таблица 3.
|
Исследуемая характеристика |
Номер рисунка |
Номер таблицы |
|
|
Частотные характеристики инерционного звена |
Амплитудно-фазовая |
3 |
4 |
|
Амплитудная |
4 |
||
|
Фазовая |
5 |
||
|
Переходная функция инерционного звена |
6 |
5 |
|
|
Частотные характеристики замкнутой системы |
Амплитудно-фазовая |
7 |
6 |
|
Амплитудная |
8 |
||
|
Фазовая |
9 |
||
|
Переходная функция системы |
10 |
7 |
|
|
Амплитудно-фазовая частотная характеристика разомкнутой системы (устойчивость по Найквисту) |
11 |
8 |
|
Оценка устойчивости системы
1.Общий метод исследования устойчивости
(по корням характеристического уравнения).
Система является устойчивой, если все вещественные корни и действи-тельные части комплексно-сопряженных корней отрицательны.
Данная система автоматического управления углом поворота тележки устойчива, т.к. все вещественные корни и действительные части комплексно-сопряженных корней отрицательны:
S1= -0,36219197418086
S2= -0,352824237286768+2,70553025613117*j
S3= -0,352824237286768-2,70553025613117*j
S4= -721.154381773435
2.Критерий Гурвица.
Главный определитель Гурвица:
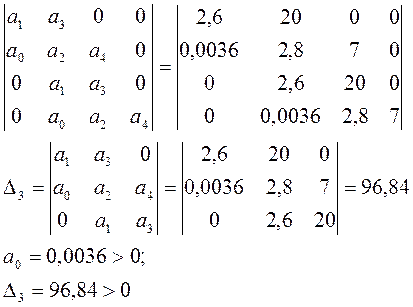
Следовательно, система является устойчивой.
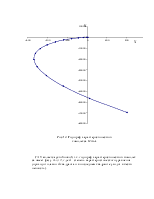
3.Критерий Найквиста.
САУ является устойчивой, т.к. годограф частотно-передаточной функции разомкнутой системы не охватывает точку (-1;0) – рис.11.
4.Критерий Михайлова.
САУ является устойчивой, если
годограф характеристического комплекса ![]() , полученного из
характеристического уравнения системы
, полученного из
характеристического уравнения системы ![]() путем
замены
путем
замены ![]() на
на ![]() ,
имеет фазу
,
имеет фазу ![]() , где
, где ![]() –
степень харак-теристического уравнения.
–
степень харак-теристического уравнения.
![]()
![]()
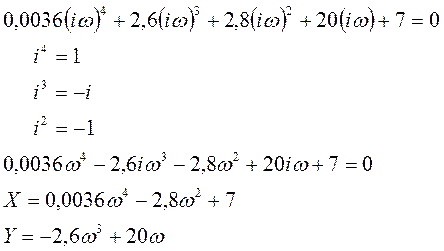


Рис.12. Годограф характеристического
комплекса ![]() .
.
САУ
является устойчивой, т.к. годограф характеристического комплек-са имеет фазу ![]() ,
где 4 – степень характеристического уравнения (проходит плавно 4 квадранта и в
последнем квадранте уходит в беско-нечность).
,
где 4 – степень характеристического уравнения (проходит плавно 4 квадранта и в
последнем квадранте уходит в беско-нечность).
Оценка качества системы
1.Запас устойчивости (рис.10):
а) Динамический заброс,%:
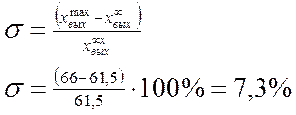
Для нормально сдемпфированных систем
![]()
б) Количество колебаний до перехода в устойчивое положение:
n=1
Для нормально сдемпфированных систем n=1…2.
в) Затухание по корню S3:
![]()
где a - действительная часть корня S3, a= -0,352824237286768
b - мнимая часть корня S3, b= -2,70553025613117
![]()
Для нормально сдемпфированных систем
![]()
г) Колебательность (склонность системы колебаться) по корню S3:
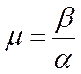
![]()
Для
нормально сдемпфированных систем ![]()
Показатель колебательности характеризует высоту резонансного пика амплитудно-частотной характеристики.
2.Быстродействие (рис.10):
а) Время переходного процесса:
![]()
б) Средний геометрический корень:
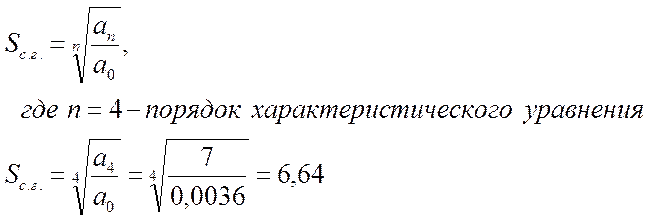
Вывод:
Запас устойчивости системы автоматического управления углом поворота тележки несколько ниже нормы. Повысить запас устойчивости можно двумя способами: путем параметрического (изменение K и T) и структурного (ввод корректирующего звена) изменения системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.